12 заметок с тегом

алгоритм Δλ

Алгоритм Δλ: ответы на вопросы

Вопросы из зала разделю на три группы: об элементарных частицах, о каркасе и общие вопросы по алгоритму.

Элементарные частицы и визуальные атомы
Спрашивает Юлия Торгашова:

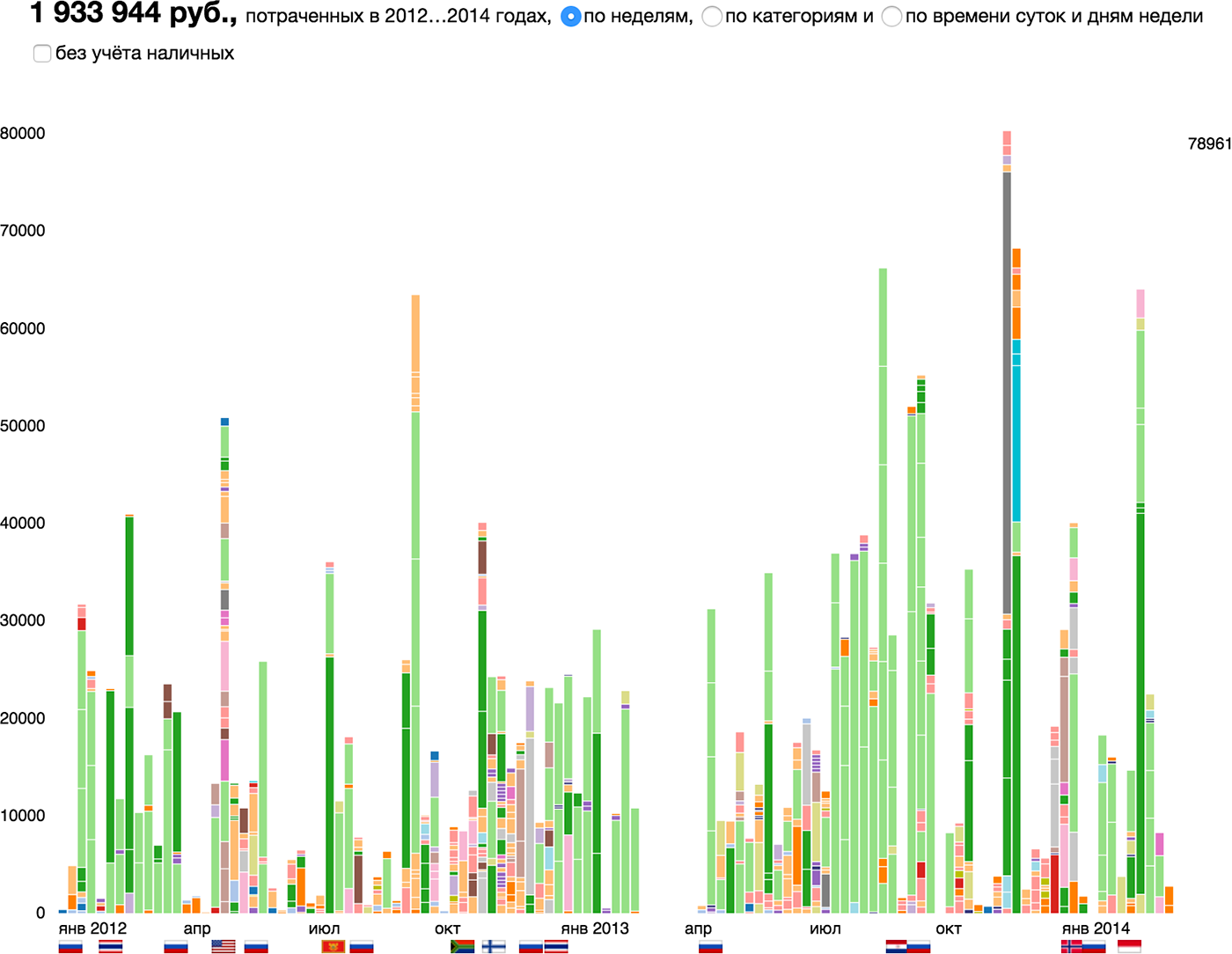
Я ломаюсь на элементарных частицах. Не могу экстраполировать на разные виды «частиц». Например, вот визуализация бюджета города, что в ней «элементарная частица» — деньги? учреждения? мероприятия? Про визуальные атомы при этом понятно.

Чтобы найти элементарную частицу нужно понимать, что искать. Элементарная частица данных — сущность достаточно крупная, чтобы обладать характерными свойствами данных, и при этом достаточно мелкая, чтобы все данные можно было разобрать на частицы и собрать заново, в том же или ином порядке.

Поиск элементарной частицы начинайте снизу вверх: ищите разные потенциальные частицы и примеряйте их к данным. «Деньги?» — хорошее начало, единица измерения бюджета, рубль, но слишком универсальная. Подойдёт, если не найдём чего-то более характерного для городского бюджет. «Мероприятия» не подходят, потому что не все бюджетные траты связаны с мероприятиями, есть и другие расходы, а элементарная частица должна описать всю массу данных. «Учреждения?» — с одной стороны, да, все бюджетные деньги можно разбить на отчисления тому или иному бюджетному учреждению. С другой стороны, это уже слишком крупная единица, ведь внутри учреждения может быть несколько транзакций, в том числе периодических. Если мы возьмём учреждение в качестве элементарной частицы, то будем оперировать только общим бюджетом этого учреждение и потеряем временной срез, а также возможный срез по целевому назначению средств.

В моих рассуждениях уже несколько раз промелькнула элементарная частица — отчисление, однократное перечисление бюджетных средств в определённом размере (те самые рубли) в определённую организацию на определённые цели (например, на мероприятия), привязанное ко времени. Отчисления бывают периодические и нерегулярные, цель может состоять из нескольких уровней иерархии: на мероприятие → на организацию концерта → гонорар исполнителя. Из отчислений состоит вся расходная статья городского бюджета, при этом отчисления можно складывать между собой, сравнивать, отслеживать динамику. Если нужно визуализировать приход бюджета, используйте частицу-близнеца — поступление. Из поступлений можно составить картину формирования городского бюджета так же, как из отчислений — картину его использования.

Попробуйте начать с низов (с единиц измерения), примеряйте на роль частицы данных всё более крупные сущности и рассуждайте, почему та или иная сущность подходит или не подходит. В рассуждениях непременно проявятся новые сущности и намёки на частицу данных. Для найденной частицы обязательно выберите подходящее слово или термин, так легче в дальнейшем думать о ней и решать задачу. Юля, пожалуйста, напишите, стало ли понятнее, и какие остались вопросы.

Спрашивает Иван Печищев:

Как соотносятся визуальная частица и частица данных? Может ли у одной частицы данных несколько воплощений в визуальных частицах? Скорее всего, да. Как они соотносятся?

В публикациях вы подробно описали визуальную сторону (пиксель, прямоугольник и т. д.). Но какой логикой я из числа (количества, расстояния и пр.) дойду до визуальной частицы? Может, элементарные частицы ввести в таблицу? Как таблица Менделеева? Чтобы было видно их отличия и схожесть. Читаешь в отдельности — понятно, сравниваешь — много похожего.

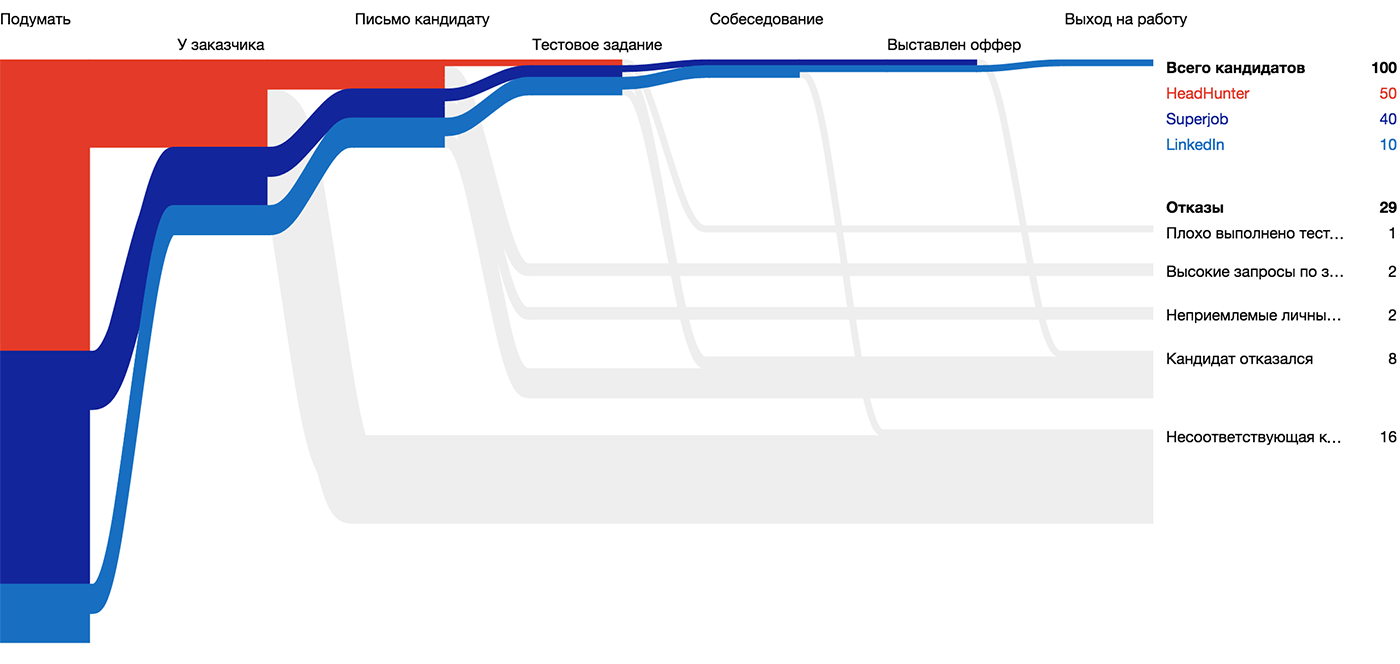
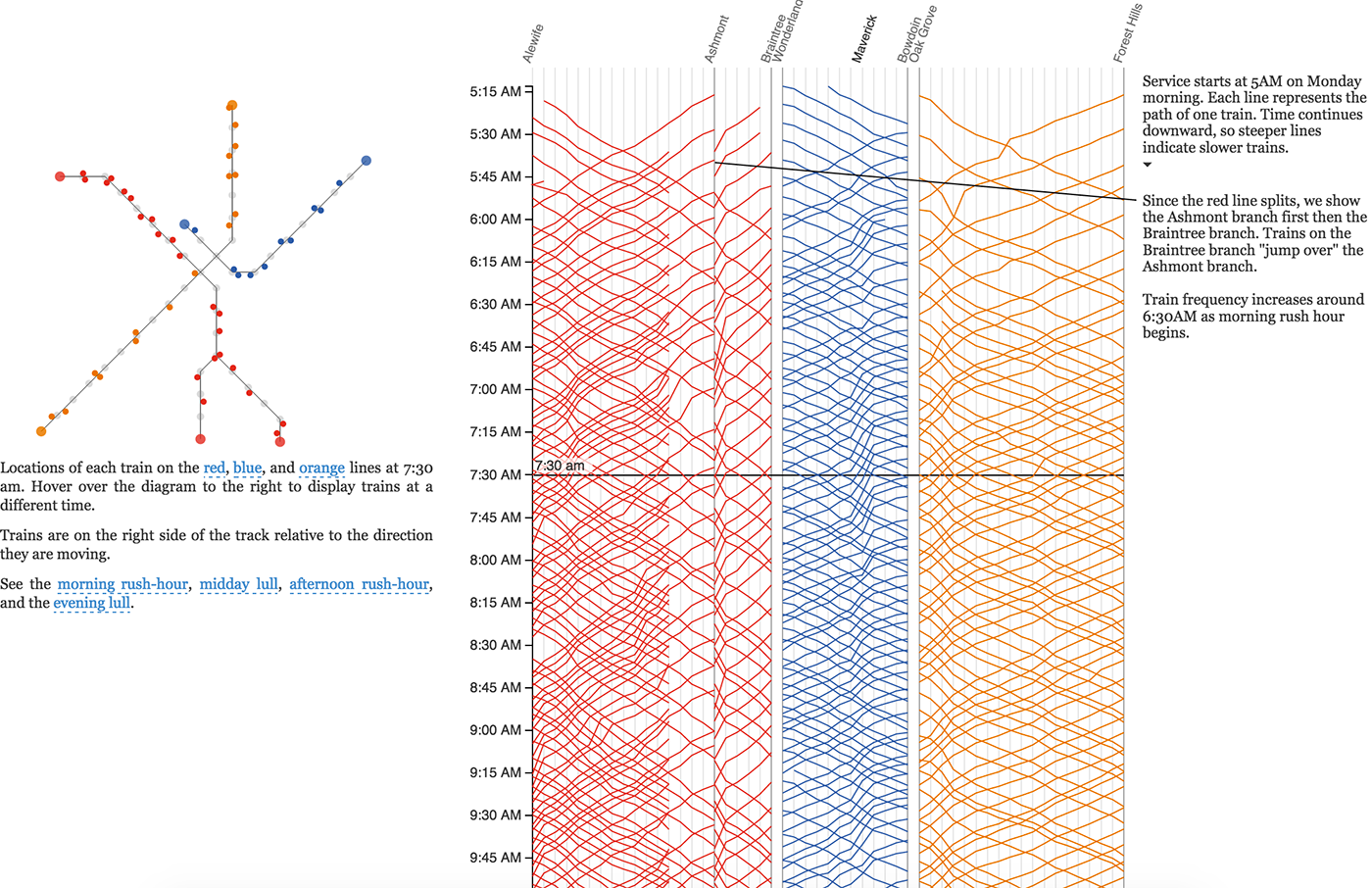
Визуальный атом — это воплощение частицы данных на экране. Одна частица данных может выражаться разными атомами. Например, путь кандидата на диаграмме «Хантфлоу» показан линией:

Мы могли бы дополнить диаграмму возрастным распределением, на котором кандидаты показаны точками:

При этом цвет частицы мы сохраняем, и разные визуальные атомы представляют одну и ту же частицу с разных точек зрения. Идея о таблице визуальных частиц — отличная, спасибо! Подумаю, как её реализовать.

Спрашивает Антон:

Я сломался после столбиковых диаграмм. Там начинается какой-то ад. Диаграмму с детскими садами вообще не понял — кажется, она прямо противоречит написанному. Либо я тупой, либо эти атомы лучше использовать с большой осторожностью :—)

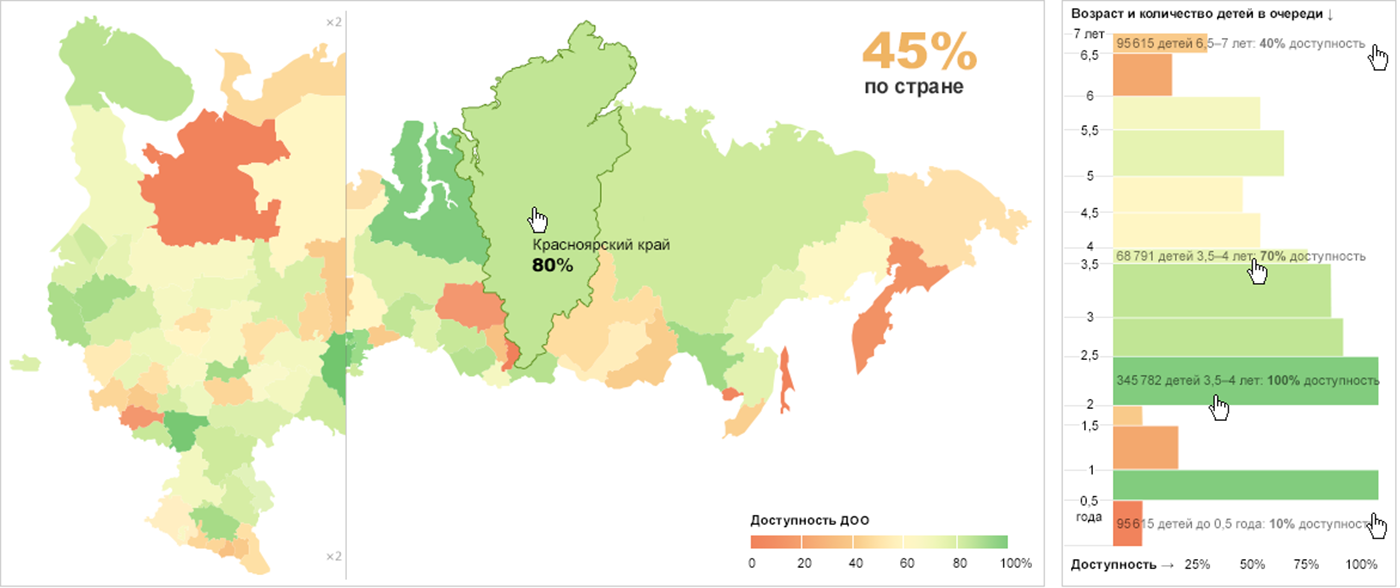
В статье речь не о формате «столбиковая диаграмма», а о прямоугольнике, как способе представления данных. У прямоугольника два линейных измерения + площадь, их производная + цвет. Прямоугольники состоят из пикселей.

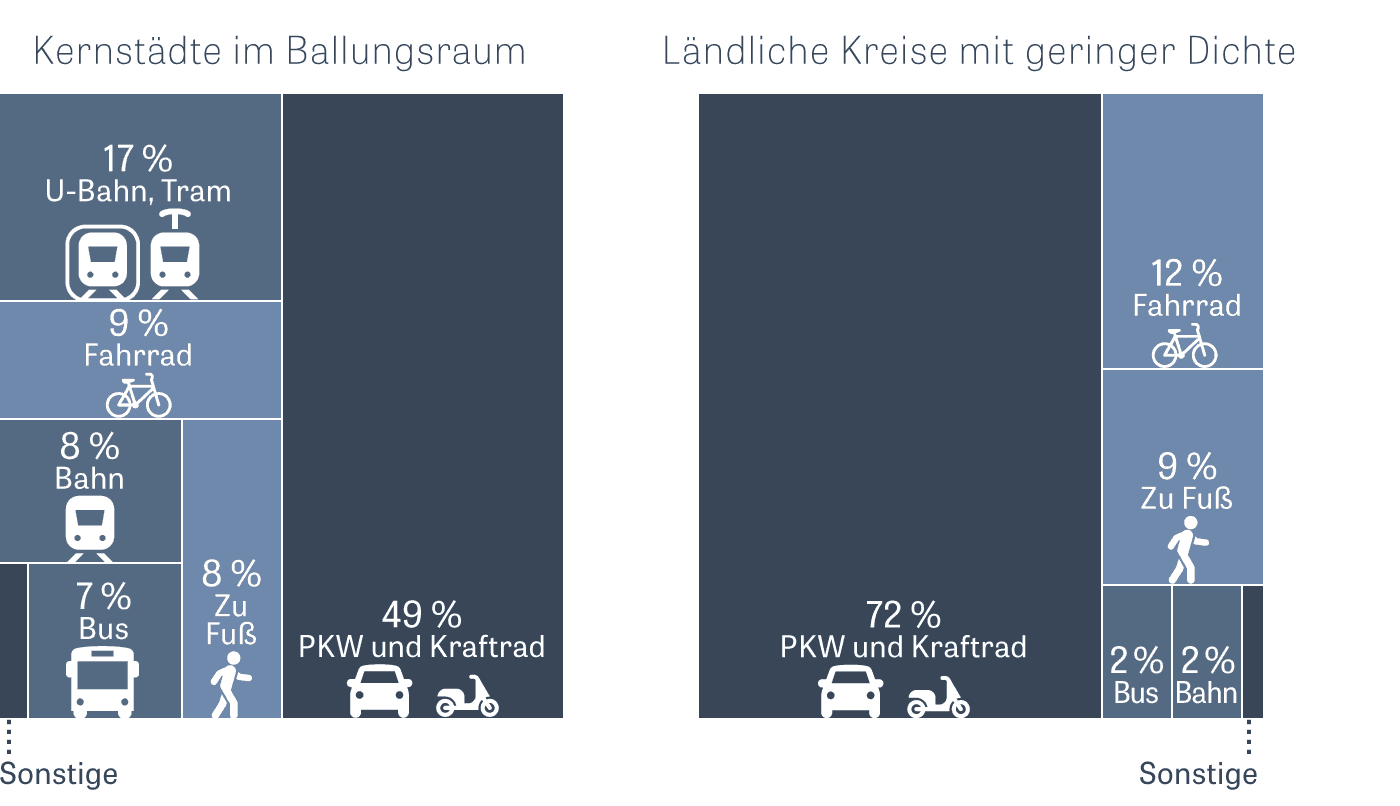
На диаграмме садиков, пиксель — это ребёнок. Группируем детей (пиксели) по возрастам, получаются прямоугольные области разного размера. Чем больше детей в возрастной группе, тем больше площадь прямоугольника. Если сделать все прямоугольники одной высоты, то их ширина отразит разницу в размерах возрастных групп. Представьте детей на площадке, пусть они станут рядом с ровесниками. Получится подобие вот такой диаграммы:

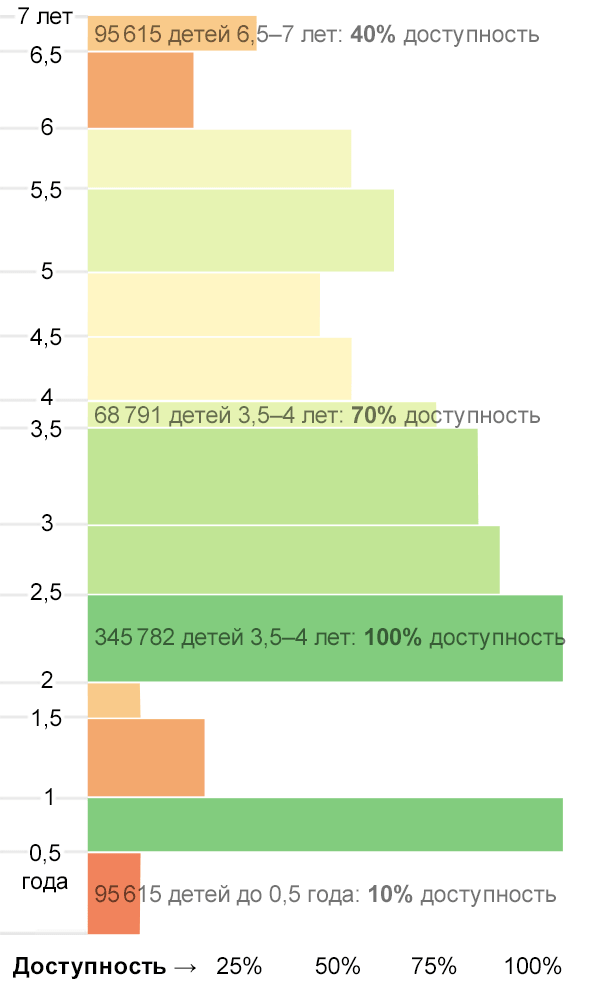
Пока за кадром остался ещё один параметр (ради которого и затевается визуализация) — доступность садиков для каждого возраста. Если мы соберём всех детей в большой прямоугольник и разделим его на слои по возрастам (чем больше детей в возрастной группе, тем толще слой), то внутри каждого слоя можно будет провести границу между детьми, попавшими и не попавшими в сад. Внутри каждого слоя появится прямоугольник попавших в сад детей, высота которого пропорциональна размеру возрастной группы, а ширина — доступности садиков для этой группы, буквально, доле попавших в сад детей.

Закрашенные столбики на диаграмме — и есть прямоугольники, попавших в сад детей разных возрастов. Можно сравнить не только доступность садов для разных групп (ширину), но и количество детей попавших/не попавших в сад (площадь). Цветовое кодирование дублирует доступность, привлекая внимание к проблемам — крупным ярким пятнам.

Ландшафт и каркас
Спрашивает Денис Балуев:

Мне, как давнему читателю, понятны почти все пункты. Кроме седьмого. Перестаю понимать отличия ландшафта от каркаса. Возможно, здесь помогли бы примеры.

Спрашивает Иван Печищев:

Очень интересен процесс «схлопывания ландшафта». Тут тоже может быть разная логика и методы. Скажем, есть технический чертёж, а есть живопись или детский рисунок.

Тему ландшафта реальности данных и каркаса визуализации я раскрою в следующей заметке, там же отвечу на вопросы.

Общие вопросы по алгоритму
Комментирует Михаил Калыгин (привожу только вопросы):

У алгоритма есть жестко заданный выход — определенного вида ответы на интересующие нас вопросы по задаче, решение задачи. В зависимости от подхода к решению вход алгоритма может быть разным. С чего здесь начинать? Какие данные нам нужны для ответа? Как определять формат этих данных? Что делать, если данных нет?

Не затронут важный шаг алгоритма — предобработка данных. Так или иначе, мы не можем работать напрямую с реальностью данных. Мы можем теоретически описать эту реальность данных. Мы можем также описать элементарные частицы. Но на практике мы имеем лишь срезы реальности, гиперплоскости, грязные данные (те же таблицы). Какие из этих грязных данных нас интересуют и могут помочь нам в ответе на вопросы задачи? Как их нужно преобразовать, чтобы нам было удобно с ними работать? Какие упрощения и допущения мы можем себе позволить в рамках этой конкретной задачи? Нужно как-то грязные данные сделать чистыми и связать с элементарными частицами и визуальными атомами. Как?

В моём понимании цель алгоритма: визуализировать конкретный набор данных с максимально пользой для зрителя. Первичный сбор данных остаётся за кадром, у нас на входе всегда есть данные. Если нет данных, то и задачи по визуализации данных нет.

Данные, с которых мы начинаем работу, — это всего лишь отправная точка. После знакомства с ними, мы представляем породившую их реальность, где данных гораздо больше. В реальности данных, без оглядки на первоначальный набор мы выбираем данные, из которых могли бы сделать максимально полную и полезную для зрителя визуализацию.

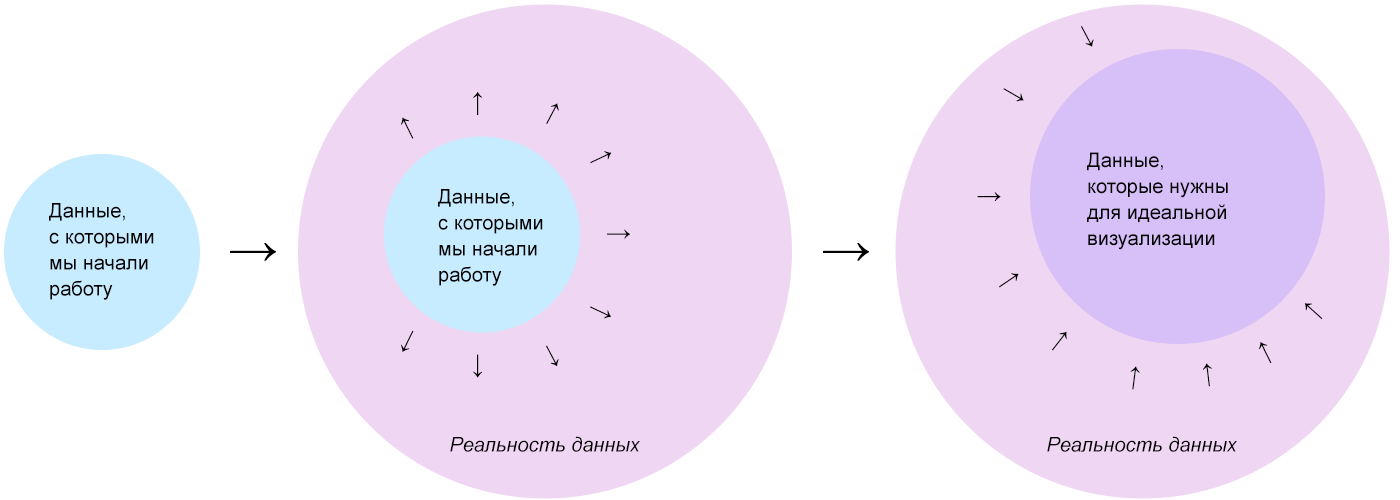
Каким будет этот набор данных для «идеальной» визуализации — зависит от сценария использования и смекалки инфодизайнера. На этом шаге лучше взять больше, чем что-то упустить. В большинстве задач уже на этом шаге вырисовывается если не вид, то основная идея визуализации.

Следующий шаг — сравнить «идеальный» набор данных с тем, что мы имеем и понять, какие из первичных данных нам понадобятся, какие — нет, и какие необходимо добыть.

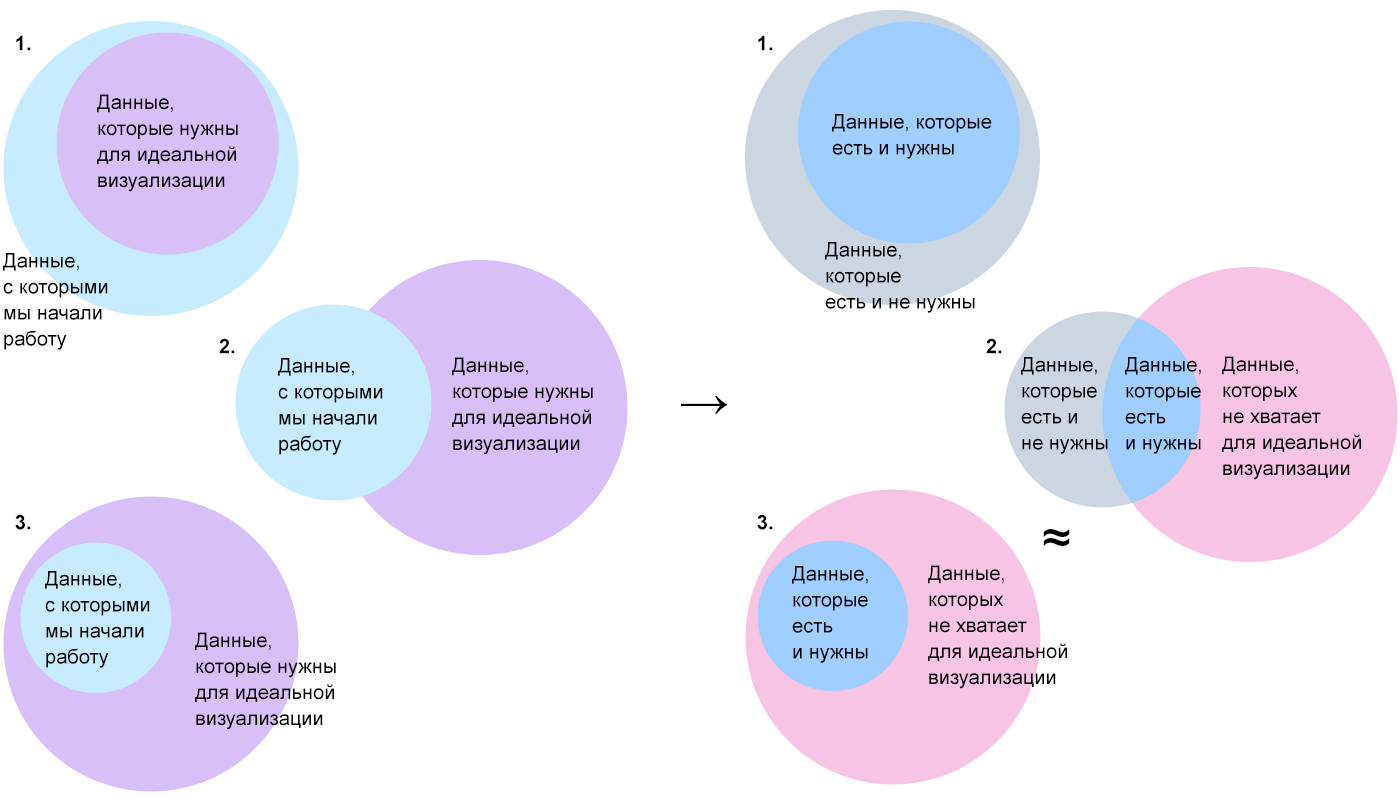
«Добыть» может означать найти, собрать или вычислить на основе имеющихся данных. Скорее всего доступными окажутся далеко не все данные «идеального» набора.

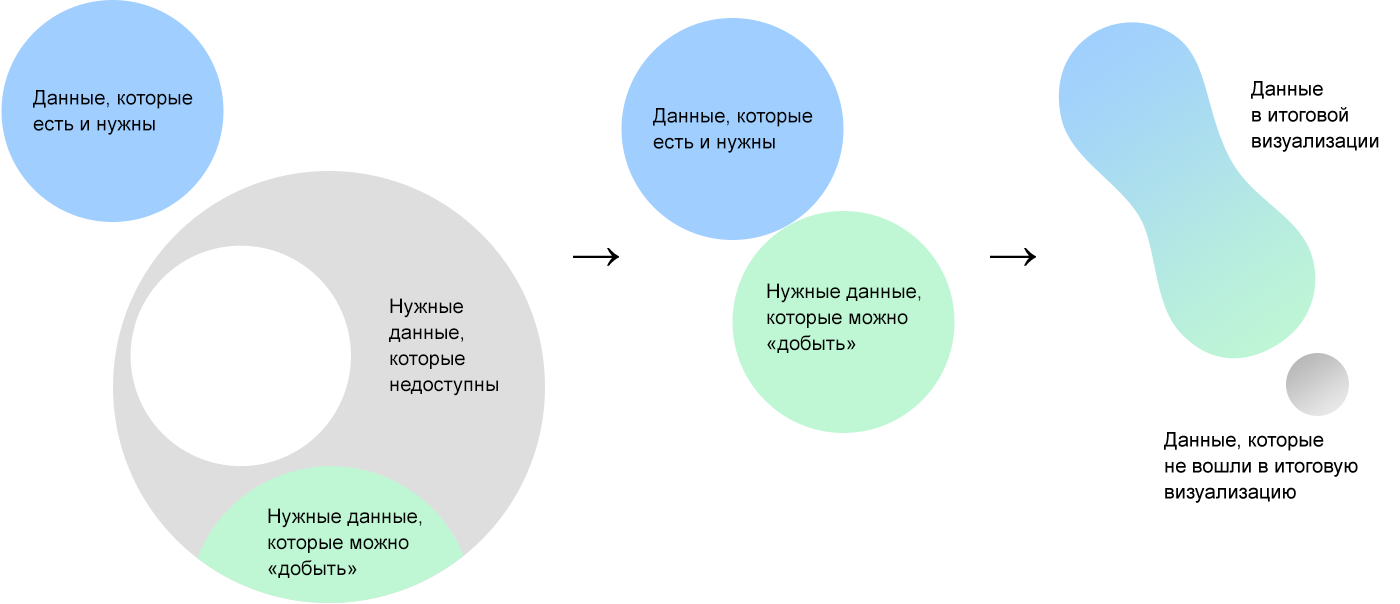
Эти данные мы и будем визуализировать. Таким образом на визуализации окажется максимально полезный из всех доступных слепок с реальности данных, а не разрозненный набор параметров.

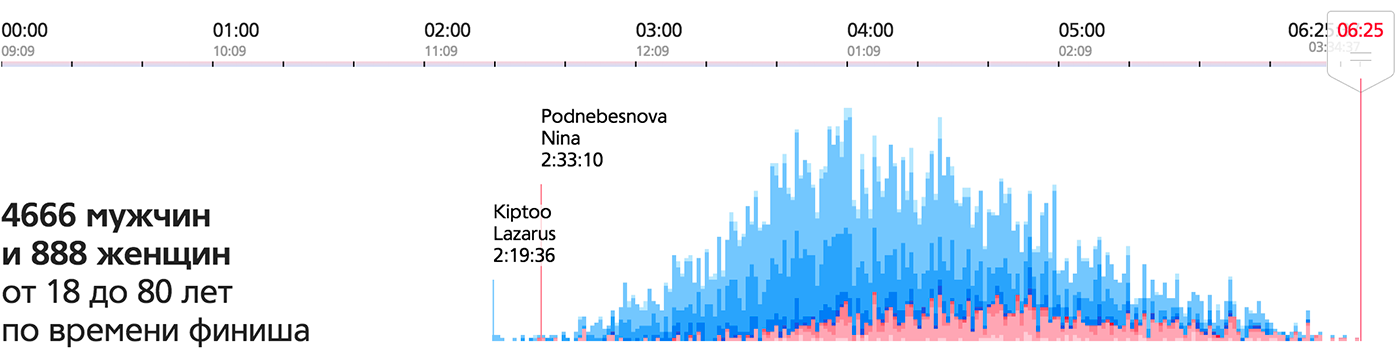
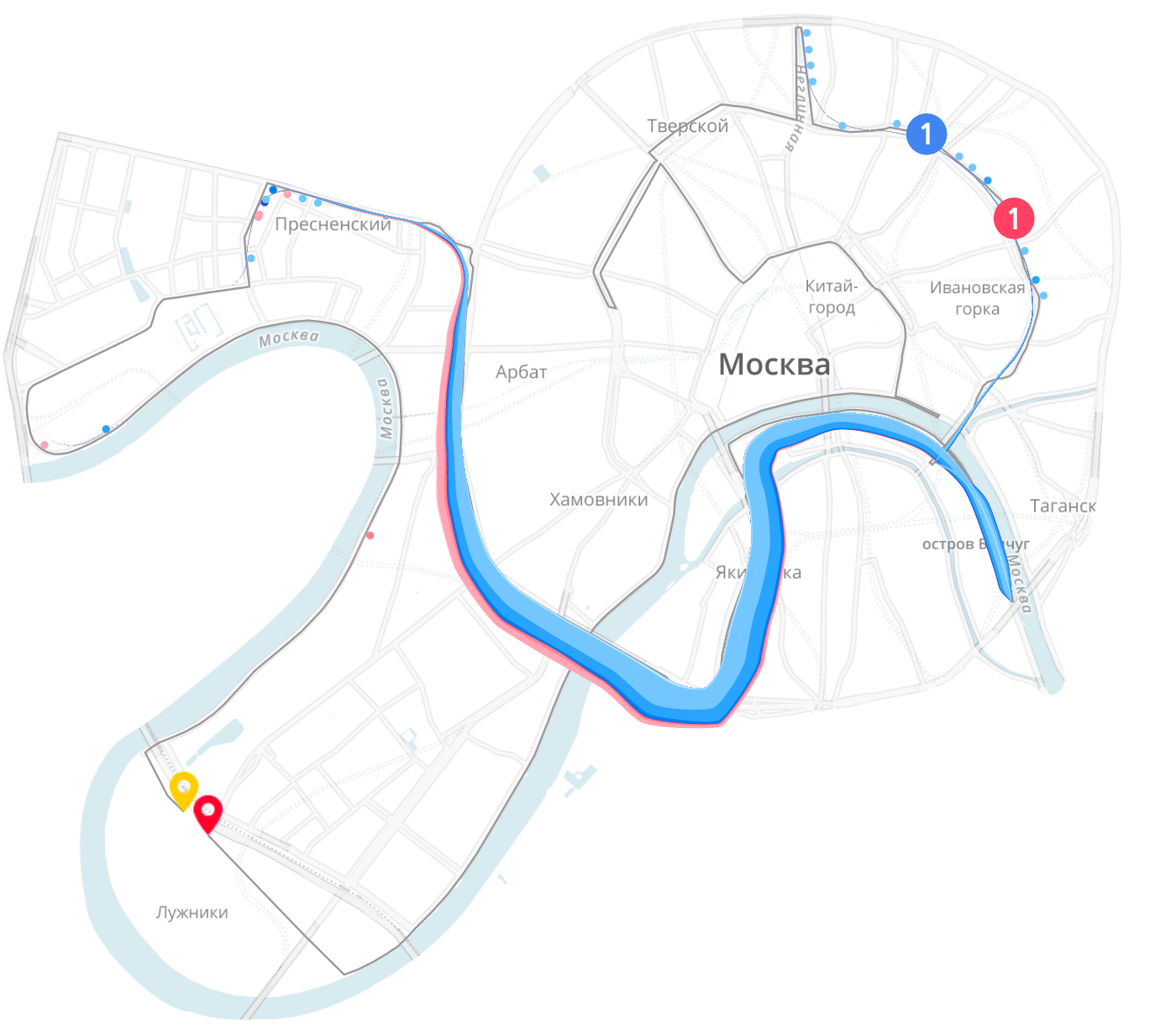
Поясню на своём любимом примере — визуализации Московского марафона. На входе у нас финишные протоколы: имя, пол и возраст участника, номер, время финиша. В реальности данных толпа бегунов, каждый со своей скоростью преодолевает марафонскую дистанцию по улицам Москвы под палящим солнцем или в дождь. Мы хотим показать процесс, как бегут люди, идеальным будет набор данных с положением каждого бегуна, его скоростью, пульсом на всём протяжении забега, изменением высоты трассы и поминутно меняющейся погодой. Подробных данных о бегунах у нас нет и в ближайшее время не будет. Есть время финиша и прохождения 3-4 промежуточных точек на дистанции. По этим точкам можно аппроксимировать положение бегунов, пишем формулы, получаем координаты и скорость бегунов в каждый момент времени. Мы допускаем такую аппроксимацию, так как на больших отрезках марафонской дистанции движение плюс-минус равномерное, то есть порядок бегунов на трассе, за редким исключением, будет рассчитан правильно. Высоту подтягиваем с картографического сервиса, погоду и ветер берём из открытых источников. Собрав все эти данные воедино, начинаем колдовать над визуализацией.

Выходит, что ответ на большинство вопросов — здравый смысл. «Какие из этих грязных данных нас интересуют и могут помочь нам в ответе на вопросы задачи?» — те, что будут полезны для зрителя и помогут ему ответить на его вопросы. «Как их нужно преобразовать, чтобы нам было удобно с ними работать?» — так, чтобы было удобно работать. «Какие упрощения и допущения мы можем себе позволить в рамках этой конкретной задачи?» — те допущения, которые не нарушают общей картины и допустимы для решения этой задачи. «Как грязные данные сделать чистыми и связать с элементарными частицами и визуальными атомами?» — преобразовать, так чтобы было удобно работать, и визуализировать наиболее близкими по смыслу визуальными средствами. На последний вопрос как раз и отвечает алгоритм.

Как и обещала, три самых вдумчивых комментатора: Иван Печищев, Юлия Торгашова и Михаил Калыгин — получают скидку 5 тыс. руб. на осенний курс по визуализации данных. Огромное спасибо всем, кто отозвался!

Следующая теоретическая заметка выйдет 19 сентября.

2016 алгоритм Δλ визуализация данных теория

Алгоритм Δλ: помощь зала

Алгоритм визуализации, который я описываю, рождается на ходу. Я начала писать теоретические заметки в феврале, не подозревая, куда этот процесс меня приведёт. С тех пор появилось 8 заметок, и каждая из них меняла мой взгляд на описанные ранее вещи. Пришло время сделать паузу, выстроить мысли в последовательную историю, обозначить белые пятна и прислушаться к читателям.

Итак, вот как я вижу процесс создания визуализации от начала до конца.

Таблицы и базы ≠ данные. Таблицы однообразны. Данные каждой задачи уникальны и живут в собственной реальности данных. Эту реальность нужно вообразить: 1, 2, 3.
Данные состоят из элементарных частиц, в одном наборе данных бывают частицы одного или нескольких видов. Каждая частица характеризуется набором свойств. Важно представлять, каков «физический смысл» этих свойств в реальности данных и как они связаны между собой.
На экране частицы данных выражены визуальными атомами (1, 2, 3), у каждого атома свой набор измерений и свойств. Визуальные атомы подбираются таким образом, чтобы полно и наглядно раскрывать свойства частицы данных. Чем ближе визуальное воплощение к физическому смыслу атрибута, тем лучше.
Множество элементарных частиц образует массу данных: сыпучую, пластичную, меняющуюся. Массой данных можно управлять: взглянуть на неё с разных сторон, разделить на подмножества так и эдак, сравнивать эти подмножества между собой. Подмножества состоят из тех же частиц данных, что и целое, ими можно так же управлять.
На экране масса данных выражена визуальной массой. Бывает, что в визуальной массе различимы отдельные атомы, в других случая они усредняются и складываются. О визуальном сложении и усреднении я ещё напишу.
Помимо массы данных, в реальности данных есть набор измерений, ландшафт, в котором живут данные.
На экране ландшафт схлопывается в одно-два-три измерения и становится каркасом визуализации. Гибкая визуальная масса легко «облепляет» жёсткий каркас, раскрываясь под определённым углом. Сложный ландшафт потребует двух и более каркасов. О видах каркасов ещё напишу.
Визуализацию дополняют интерфейсом для управления массой данных (например, выборки и поиск) и каркасом (например, настройка осей). Об интерфейсной обёртке визуализации ещё напишу.

Я боюсь, что мои рассуждения слишком абстрактны и непонятны даже тем, кто искренне интересуется темой. Я хочу сделать заметки полезнее, но мне сложно взглянуть на результат со стороны, поэтому я прошу помощи читателей. Напишите, что вам непонятно, где вы теряете нить, с чем не согласны. В следующей заметке я разберу все комментарии и отвечу на ваши вопросы. Коллективный разум, отзовись!

Иллюстрация Йоко Д’олбачи

Следующая теоретическая заметка выйдет 5 сентября.

2016 алгоритм Δλ визуализация данных теория

3 комментария

Алгоритм Δλ: визуальные атомы, часть 3

Заключительная заметка о визуальных атомах (первая и вторая части). Сегодня поговорим о мини-графиках и картографических атомах.

Мини-графики
Иногда смысловой частицей данных, которую мы изучаем и сравниваем, является не единичное значние, а набор или серия значений. На прошедшем в апреле учебном курсе один из студентов визуализировал показания датчиков, контролирующих производственные процессы. Десятки датчиков измеряли различные величины иногда с частотой раз в секунду. В такой ситуации формально квантом информации является отдельное измерение, но осмысленной частицей данных будет «поток», то есть последовательность значений с каждого датчика. Потоки визуализируются мини-графиками, из которых складывается общая картина и которые можно сравнивать между собой. Вот грубая иллюстрация на примере схемы Регуляра — реальное расположение приборов и визуализация:

Вид мини-графика зависит от измеряемой величины, можно отметить минимумы, максимумы и допустимый диапазон

На визуализации занятости жителей Миннесоты хорошо видна сезонность в одних отраслях, рост и спад в других:

Видно появление и исчезновение таинственной отрасли Animal Aquaculture и космической программы — Space Research and Technology, в полной версии на сайте

Для удобства чтения все графики имеют одинаковую высоту в максимальной точке, соответсвенно разный масштаб. Конкретные значения показаны при наведении.

Частота употребления слов в официальных обращениях американских политиков:

Резкие пики сопровождаются пояснениями редакции

Климат разных городов на визуализации температурных рекордов, сравниваем толщину (разброс температур) и окраску (конкретные значения относительно нуля):

Активность у своих и чужих ворот, слабые и сильные стороны команд на визуализации голевых моментов:

Мини-графики хороши для больших наборов значений со стройной иерархией внутри. Осмелившись показать все значения, не усредняя и не обедняя выборку, вы получите информационно насыщенную, интересную для изучения визуализацию.

Географические атомы: точка, объект, область, маршрут

Визуальные атомы на карте могут быть точечными (точки, круги, объекты), площадными (области) и протяжёнными (линии).

Точки на карте — это места, события и объекты с конкретными координатами. В зависимости от масштаба карты точка может быть квартирой в доме на конкретной улице или целым городом.

Например, квартиры, сдающиеся через «Эйрбнб»:

Уже знакомые нам землетрясения:

И полезные/вредные приёмы пищи, слившиеся в облака:

Сложенные стопками смертельные случаи заболевания холерой на знаменитой карте Джона Сноу:

Дома Москвы, родом из разных эпох:

Достопримечательности на карте-путеводителе:

Точечные объекты на карте передают информацию своим положением, цветом, размером, а также засчёт подписей и картинок. Если данных для каждого объекта слишком много, располагать их на карте будет не лучшим решением. Карта диктует жёсткую топологию, и экранное пространство используется неэффективно. В таком случае я советую показать данные в виде мини-графиков, а карту использовать как дополнительный справочный элемент:

При наведении на мини-график город на карте подсвечивается красным.

Площадные объекты — это области на карте: городские кварталы, районы, округа, страны и другие государственные территориальные единицы, а также геологические и географические регионы. Площадные объекты передают сводную информацию по территории, чаще всего с помощью цветной заливки.

Однотонная показывает один параметр, например, высоту застройки или стоимость земли на Манхэттене:

Двухцветная — близость к полюсам шкалы:

Заливка полупрозрачными слоями делает акцент на пересечении накладывающихся друг на друга областей:

Границы районов Бостона, как их видят жители

На карте затопления Венеции площадная заливка улиц и площадей сочетается с точечной окраской пострадавших от наводнений зданий:

Карта может быть настоящим произведением искусства, с большим количеством цветов и оттенков:

Геологическая карта Пенсильвании

На «карте здоровья» части света покрыты паттерном человеческих тканей и клеток, поражаемых самой распространённой там болезнью:

Северная Америка покрыта жировой тканью, Европа — мозговыми нейронами (слабоумие), Африка — кровяными тельцами (малярия и СПИД), на страдающей от бесплодия Гренландии изображены сперматозоиды

Вместо заливки иногда используются изолинии, как на этой карте запахов Эдинбурга:

Протяжённые объекты на карте — это путевые сети, маршруты, границы, а также реки и горные цепи. Связанные с ними данные визуализируются линиями и змейками разной толщины, цвета и яркости.

Классическая карта Шарля Минара показывает объёмы экспорта угля Англией:

Поток делится на крупные рукава, потом на более мелкие — в соответствии с морскими путями доставки угля

Суточное движение швейцарских поездов:

Цветом линии показана скорость поездов, толщиной — их загруженность

Ветра в Токио в режиме реального времени:

Чем длиннее линии, тем сильнее дует

Воздушные пути на разной высоте над городами мира:

Высота полёта закодирована цветом

Поток беженцев из разных стран:

Чем больше поток, тем ярче луч

Вся пресная вода земного шара, как на ладони:

Сразу видно, где густо, а где пусто

При визуалиции геоданных важно учитывать характер данных и выбирать соответсвующие визуальные атомы. Привязывать точечные данные к областям, а сводные параметры по целым регионам или протяжённым объектам отображать точками, на мой взгляд, грубая ошибка.

Следующая теоретическая заметка выйдет 8 августа.

2016 алгоритм Δλ визуализация данных визуальные атомы теория

Алгоритм Δλ: визуальные атомы, часть 2

Продолжение заметки о визуальных атомах. Сегодня поговорим о прямоугольниках, отрезках и линиях.

Прямоугольник
Прямоугольники обладают четырьмя собственными свойствами (ширина, высота, их производная — площадь, цвет) и легко складываются друг с другом.

Прямоугольники единичной ширны складываются в столбиковую диаграмму:

Элементарная частица в личных финансах — трата, визуальный атом — прямоугольник единичной ширины, его высота соответствует размеру траты, цвет — категории. На диаграмме траты суммируются, высота столбика показывает размер недельных трат.

Элементарная частица продаж интернет-магазина — продажа, визуальный атом — прямоугольник единичной ширины, его высота соответствует сумме продажи. Высота столбика на диаграмме показывает суточную выручку. Цветом показаны будни и выходные дни.

Прямоугольники подходят для отображения групп элементов (чаще неразличимых пикселей, редко — точек), в этом случае ширина и высота прямоугольника задействуются для визуализации параметров группы. Важно выбирать параметры для ширины и высоты так, чтобы их произведение — площадь, также имело физический смысл.

Например, если количество детей в возрастной группе задаёт высоту прямоугольника, а доступность садиков для этой группы — его ширину, то площадь прямоугольника соответсвует количеству детей этого возраста, попавшему в сад.

Видим, что проблема для группы 1,5-2 года стоит острее, чем для группы 2-2,5 года — хоть доступность садов в ней и выше, но нуждающихся в садике детей намного больше.

По такому же принципу прямоугольники образуют квадратные и тримэп-диаграммы:

Отрезок
Отрезок визуализирует частицу данных, состоящую из двух связанных элементов.

Это может быть связь двух объектов, например, брачный союз людей разных профессий:

Связь «до и после» двух значений одного и того же параметра, например, количество высокооплачиваемых должностей в различных индустриях:

.
Связанные попарно значения, например, результаты ответов на вопросы теста, личный и средний по соотечественникам:

Или пара связанных пространственных координат, например, начальное и конечное положение мяча при ударе по воротам:

Линия
Линия показывает путь или историю объекта во времени. Для линии важны не только точка начала, точка конца и связь (как в отрезке), но и форма пути между ними. Линии сливаются в потоки и делятся на русла.

Частица данных — кандидат, проходящий этапы воронки собеседований

Частица данных — штат, изменяющий свои настроения во времени

Частица данных — поезд метро, движущийся между станциями

Частица данных — заключённый, проводящий срок в тюрьме Гуантанамо

Частным случаем линии является географический маршрут.

Частицы данных — французы армии Наполеона, наступающие на Москву и отступающие обратно

О мини-графике и географических атомах (точке, области, объекте и маршруте) я расскажу в третьей, заключительной заметке.

Следующая теоретическая заметка выйдет 4 июля.

2016 алгоритм Δλ визуализация данных визуальные атомы теория

1 комментарий

Алгоритм Δλ: визуальные атомы, часть 1

Сегодня я расскажу о наглядном визуальном кодировании частиц, из которого естественным образом вырастает содержательная и наглядная визуализация.

После ответа на вопрос о том, что является элементарной частицей данных, задумайтесь, как её лучше всего показать. Элементарная частица данных — это визуальный атом, и её воплощение должно быть атомарным. Основные визуальные атомы: пиксель, точка, круг, черта, квадрат, ячейка, объект, прямоугольник, отрезок, линия и мини-график. Выбор атома следует из свойств частицы данных и её поведения в реальности данных.

Пиксель
Пиксель — минимальная экранная единица, пиксели обозначают «безликие», неотличимые друг от друга частицы, которые сливаются в единое целое, например, бюджет страны, стоимость товаров и услуг, дефицит личного бюджета, бюджет фильма или результаты опроса. Пиксели суммируются в столбцы, прямоугольные области и потоки, площадь которых пропорциональна сумме частиц данных.

Эффективность предприятия в прошлой заметке также складывается из пикселей — тонн продукции:

Точка
В отличие от пикселя, точка кодирует отдельные, явно различимые объекты: спортсменов, рядовых американцев, сотрудников, температурные рекорды, землетрясения, медалистов, приёмы пищи и т. п. Цвет точек отражает качественную или количественную характеристику.

В простом случае точки занимают свои позиции и отображаются на графике по отдельности:

Медалисты всех олимпиад в беге на 100 м

Годовая зарплата и результативность ведущих американских бейсболистов (по командам)

Активность американцев в разное время суток

Иногда точки соединяет кривая:

Если точки необходимо просуммировать, способ визуального суммирования зависит от характера данных.

Для складывания элементов в стопки в одном измерении подходят чёрточки:

Для составления столбиковых диаграмм используют квадратики:

Иногда точки просто накладывают друг на друга с прозрачностью, в таком случае яркие точки показывают наиболее распространённые значения:

Температурные рекорды в РФ

Землетрясения с 1898 года

Большое количество точек сливают в круги, потоки и облака, в них точки перестают быть различимыми:

Визуальное сложение мы обсудим подробнее в следующих заметках.

Круг
Круг помимо цвета и расположения имеет радиус, который кодирует дополнительное измерение данных. Классический пример элементарных частиц-кругов — страны на Гэпмайндере, где изменяющийся со временем радиус круга показывает рост популяции:

Здесь частицей данных является страна, в отличие от рассмотренного выше примера с олимпийскими медалями, где элементарной частицей является медаль, и уже медали суммируются в круги-страны.

Другие примеры:

Круги — крупные американские компании, радиус показывает их «вес» (рыночную стоимость), цвет — размер налоговой ставки

Круги — картины Пабло Пикассо, радиус показывает стоимость проданных на аукционах картин, цвет — тип (масло/акварель-гуашь)

Ячейка
Ячейка — это элемент регулярной сетки, как правило, квадратной формы. Линейные размеры ячейки не имеют значения. Частицы данных распределяются по сетке, а их свойства суммируются или усредняются и отображаются цветом ячейки.

Суммирование может быть примитивным (чем больше, тем ярче):

Или оценочным, например, с использованием светофорного градиента «хорошо-плохо»:

В этом примере на одной сетке просуммированы сон и ходьба городских жителей:

Объект
Роль точки на графике может играть реальный объект. В этом случае к свойствам, показанным на графике, добавляется наглядная информация с изображения объекта.

Классический пример Эдварда Тафти — график соотношения массы мозга и массы тела с животными вместо точек. Легенда не требуется: