Пандемия коронавируса затронула почти все страны. Человечеству впервые выпадает шанс наблюдать нечто настолько глобальное, при этом касающееся каждого, и держать руку на пульсе с помощью современных технологий. Исследователи строят математические модели, которые учитывают поведение широких масс, и наблюдают в режиме реального времени, как эти прогнозы сбываются. Но что ещё важнее, они показывают свои модели тем самым широким массам, которые самостоятельно делают (или не делают) выводы, меняют (или не меняют) поведение и, как следствие, в какой-то мере определяют сценарий развития ситуации.
Сейчас, как никогда, важно не просто наблюдать процесс, но и доносить наблюдения и выводы учёных до обывателей. От способов представления данных, их прозрачности и наглядности, доверия к ним — от сообщения, вложенного в ту или иную визуализацию, зависит будущее, которое всех нас ждёт.
Поделюсь визуализациями, которые произвели лично на меня самое большое впечатление и сильнее всего повлияли на мои собственные решения.
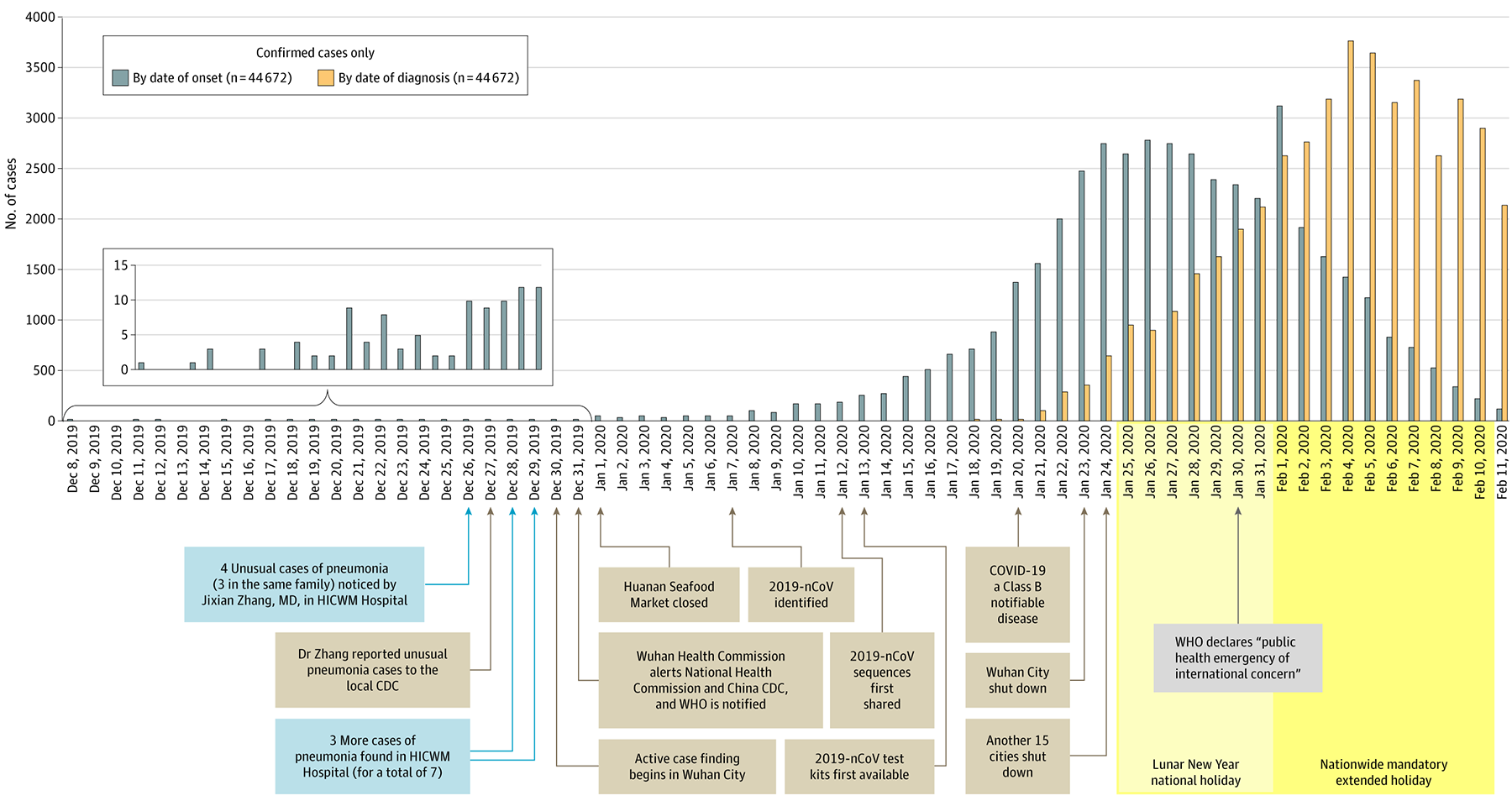
График количества заболевших из статьи «Особенности и уроки вспышки коронавирусной инфекции — 2019 (COVID-19) в Китае», опубликованной 24 февраля в журнале Американской медицинской ассоциации, чаще всего цитируется в контексте «скрытой угрозы». И не случайно. Это гениальная в своей простоте визуализация показывает, что каждый обнаруженный случай заболевания, особенно в самом начале эпидемии, был диагностирован с задержкой около двух недель. Синие столбики — истинное количество заболевших, жёлтые — поставленные диагнозы. Подробный анализ графика можно почитать в оригинале и по-русски. Отмечу лишь главную мысль за этими данными: «Реального количества заболевших на данный момент не знает никто».
Другой впечатляющий формат — толпа корейцев, прихожан церкви Шинчионджи, самый обширный из корейских кластеров распространения короновируса:
Предположительно, вирус попал в церковное сообщество через единственную женщину, известную как «31-я пациентка», которая дважды посетила церковную службу, уже после появления симптомов и временной госпитализации, но до постановки диагноза. Мы видим каждого человека из 5016 инфицированных (вспомним визуализацию потерь Второй мировой войны). И, зная, что на данный момент 162 человека в Южной Корее погибли, можем представить это не как абстрактную цифру, а как реальные прервавшиеся жизни людей, в лицо которым мы как будто смотрим на этой визуализации. И цифра уже не кажется такой уж незначительной, какой она выглядит на общем трагическом фоне.
О том, как вирус распространился внутри Китая и по миру, обгоняя запаздывающие карантинные меры, лучше всего, на мой взгляд рассказывает Нью-йорк-таймс. Невероятно красивая и достаточно аккуратная визуализация, местами настоящее произведение искусства:
Обратите внимание, что здесь показаны либо статистически предполагаемые случаи, либо достоверно зафиксированные в будущем и отмеченные на карте «задним числом». Это даёт более-менее адекватную картину происходившего, аналогично графику выше. Ключевое слово здесь — происходившего. Картины происходящего прямо сейчас, как я писала выше, мы не знаем.
Отсюда проблемы с таблицами и картами, самыми популярными на данный момент форматами представления данных о текущей ситуации. Поговорим о них.
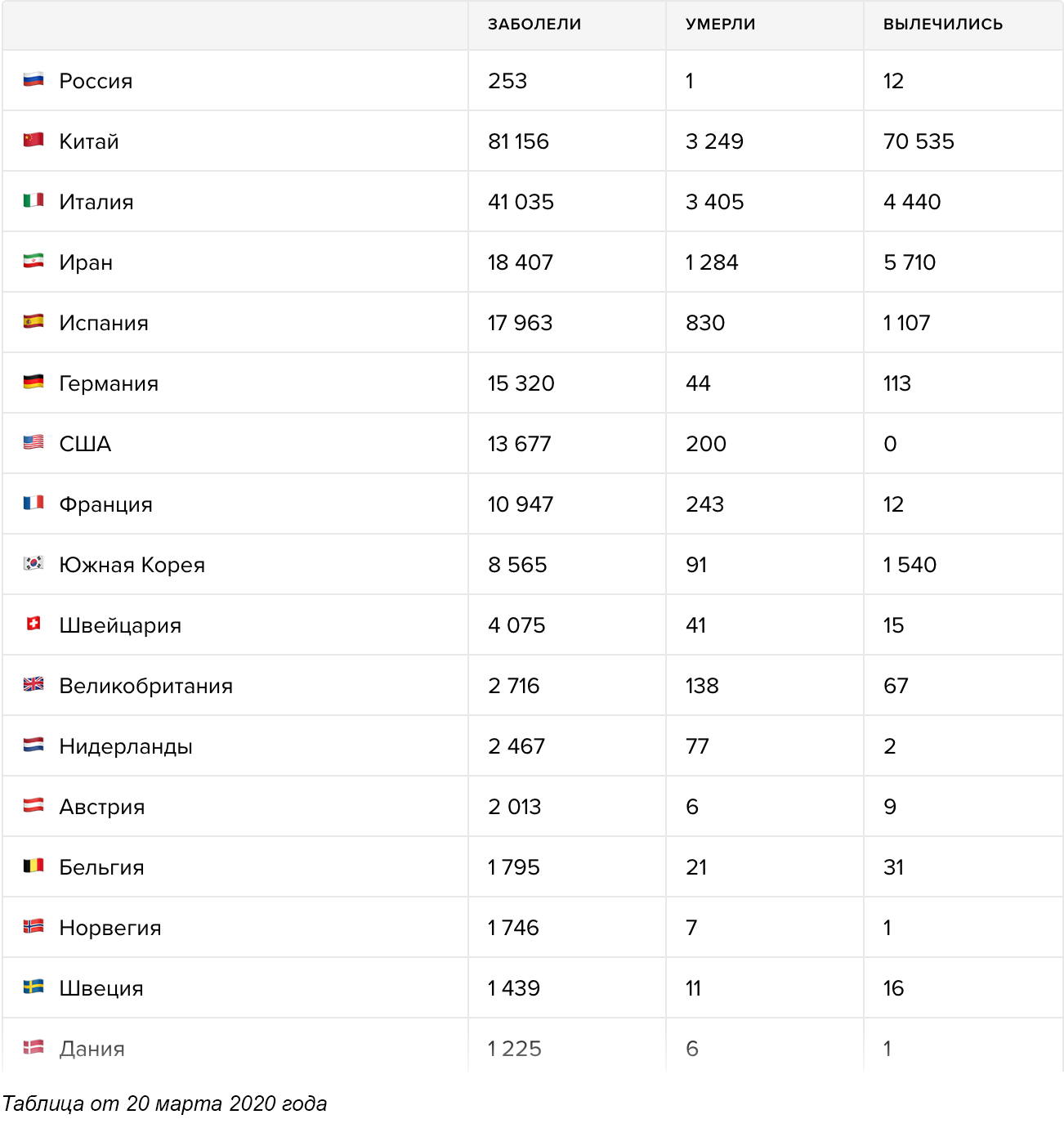
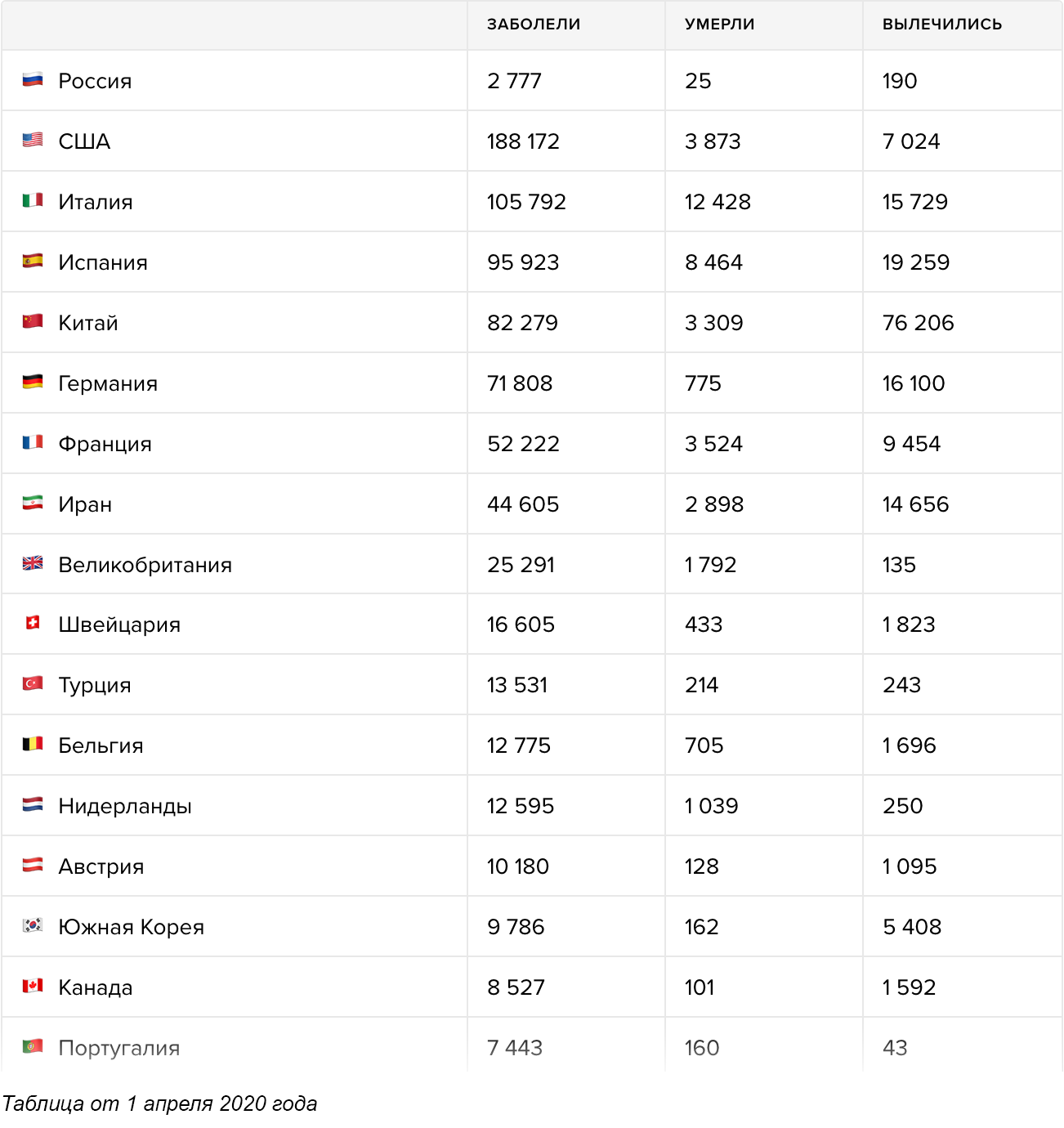
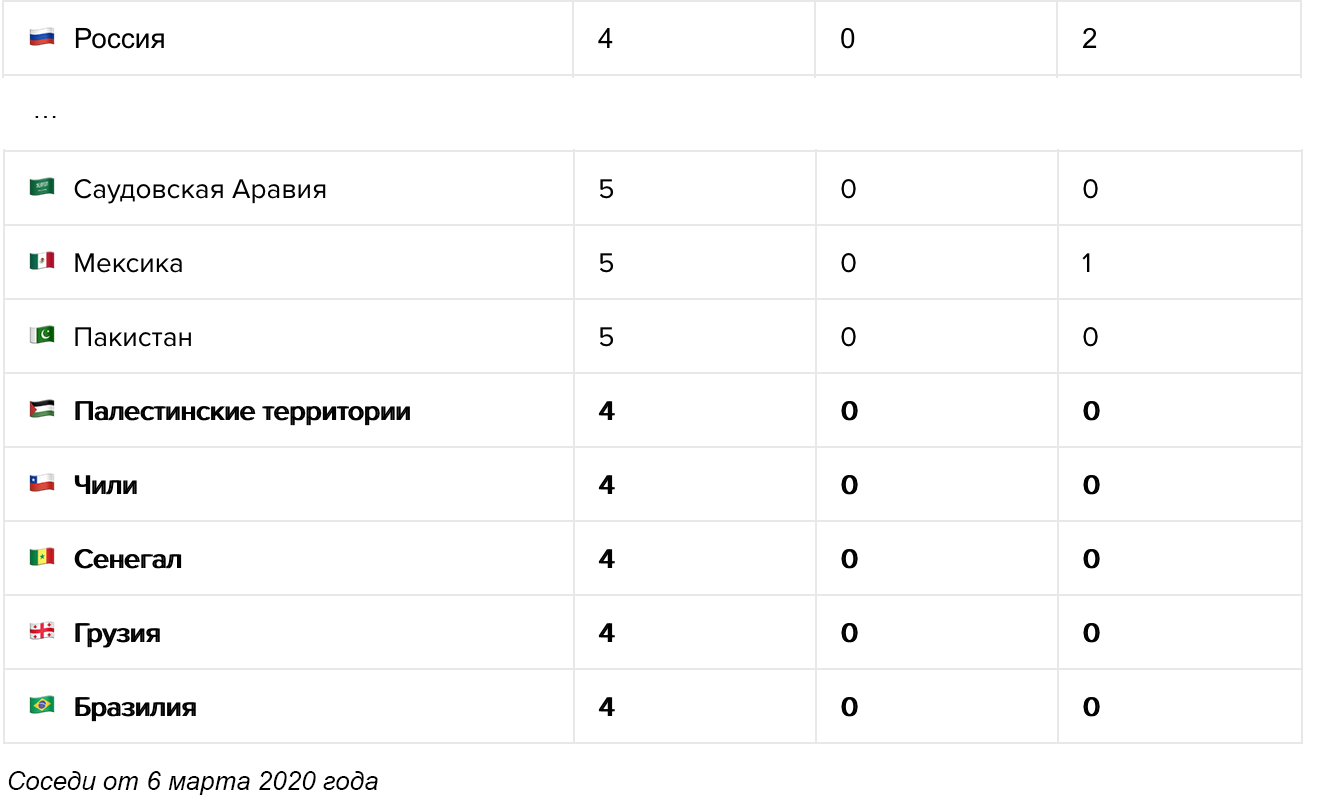
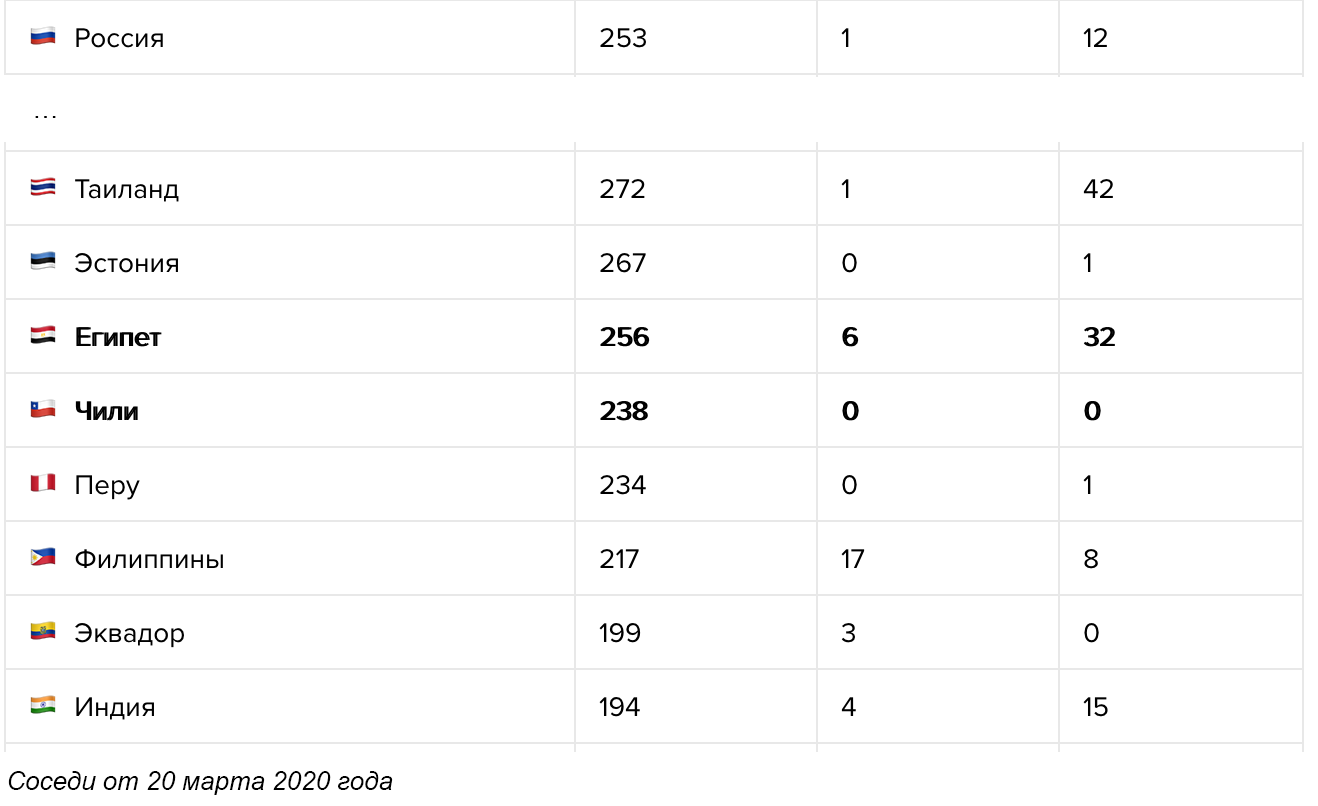
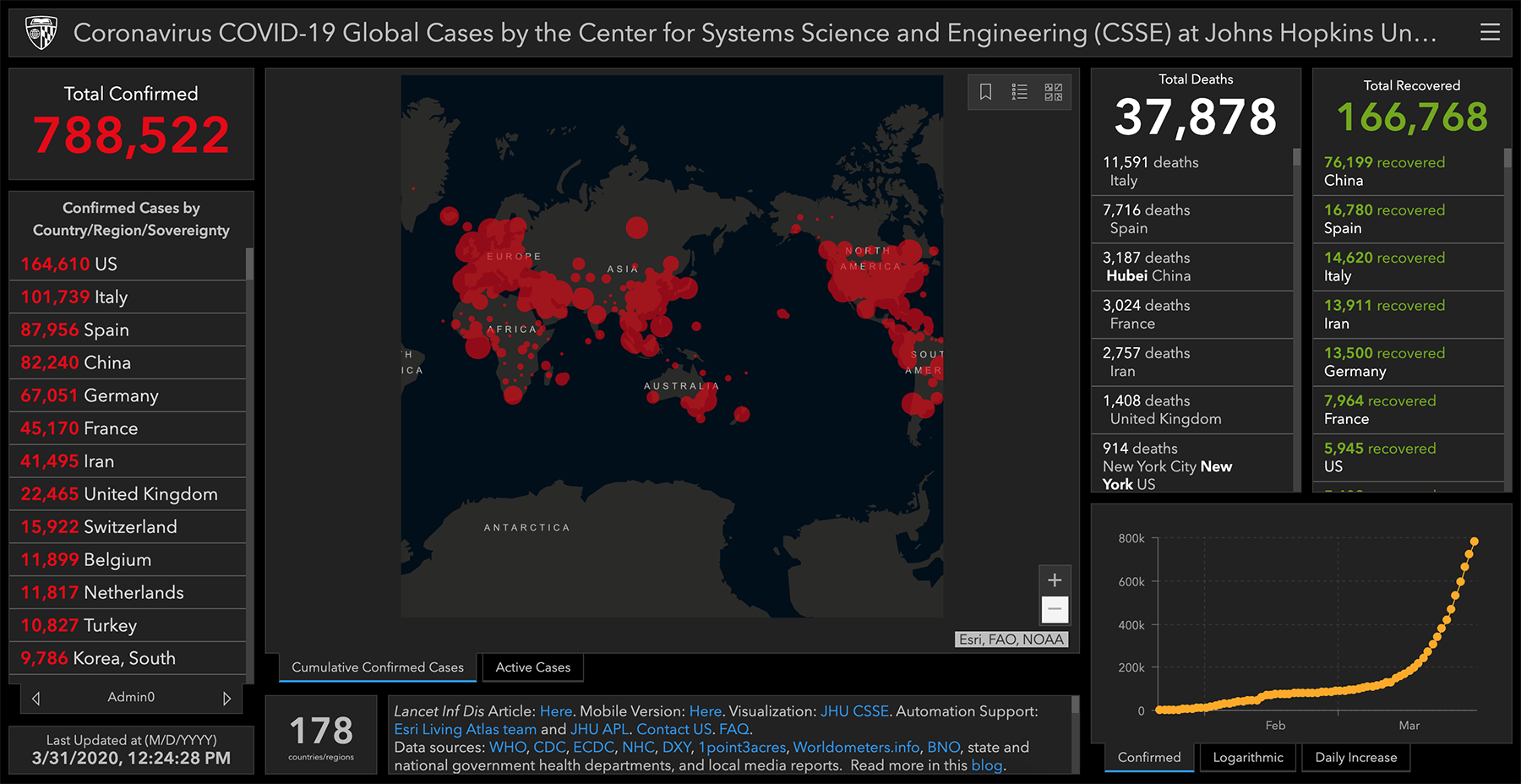
Университет Джона Хопкинса — один из самых надёжных источников данных о положении дел в мире. Но их карта, как и все остальные карты на сайтах всех новостных площадок, организаций и министерств здравоохранения, не говорит буквально ни о чём. Во-первых, процедуры тестирования в разных странах отличаются, и сравнивать Германию с массовыми тестированиями и Италию, в которой тесты проводят только больным с симптомами, просто бессмысленно. Во-вторых, данные по странам отличаются настолько сильно и меняются так быстро, что заметить важные изменения в формате карты просто невозможно. В-третьих, карта не выполняет свою основную функцию — она не показывает текущее положение дел. Данные о количестве подтверждённых случаев не отражают ситуацию и могут отличаться от истинного количества заболевших в разы и даже на порядки, в зависимости от процедуры тестирования и карантинных мер в отдельно взятой стране. При этом обычные люди, глядя на карту и изучая цифры с точностью до одного заболевшего, как правило, не отдают себе отчёта в том как сильно эта «текущая ситуация» отличается от истинного положения дел.
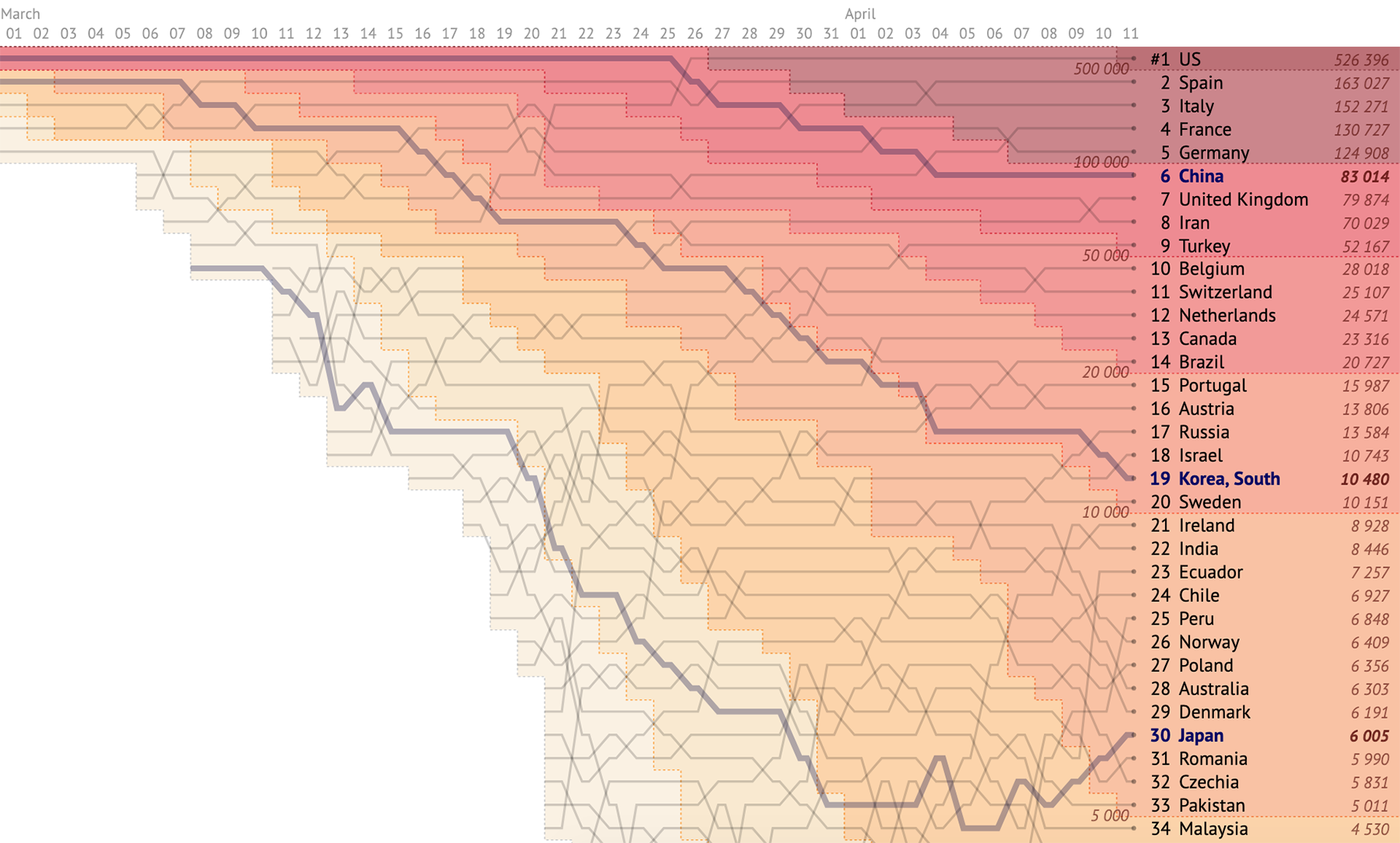
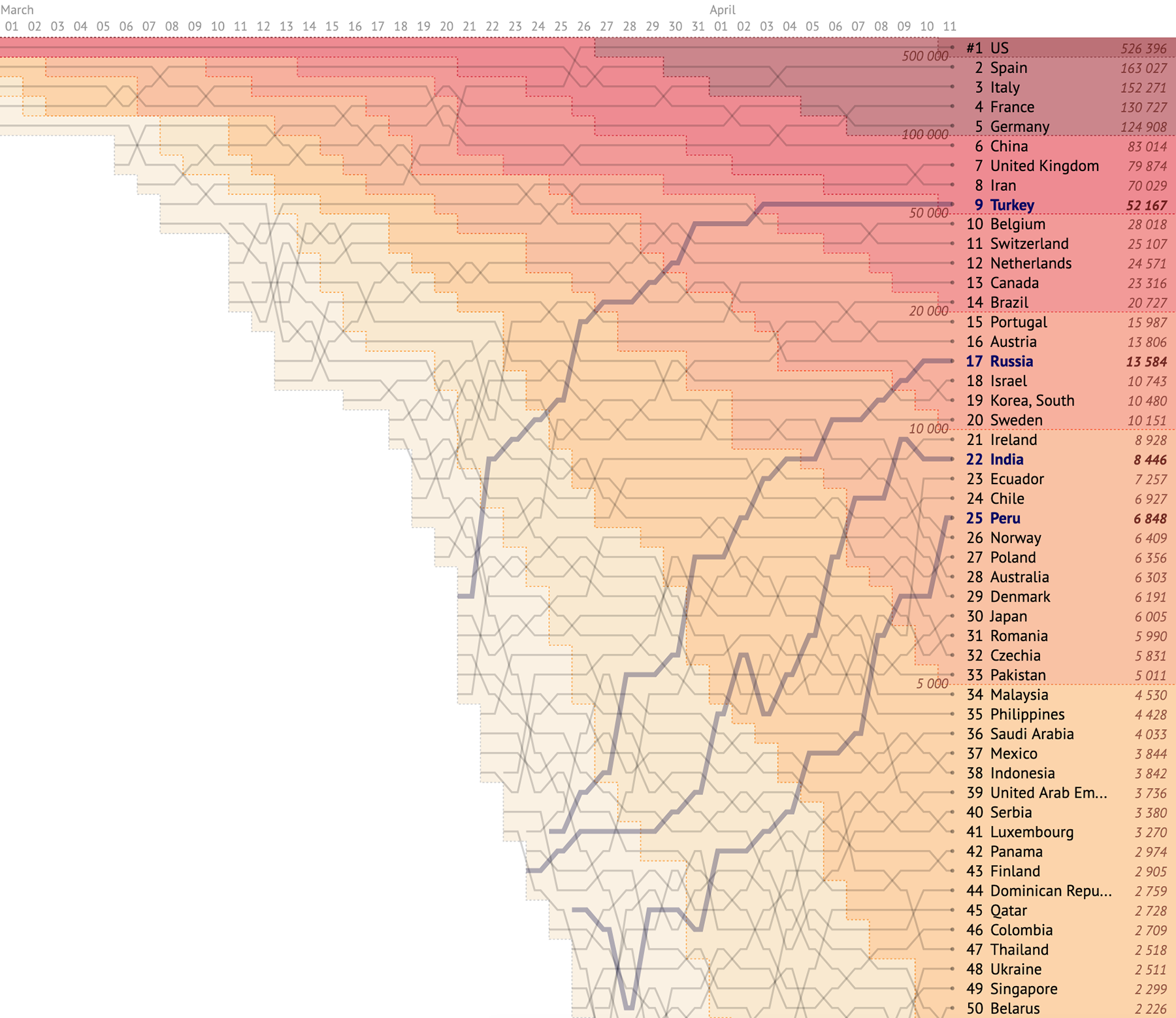
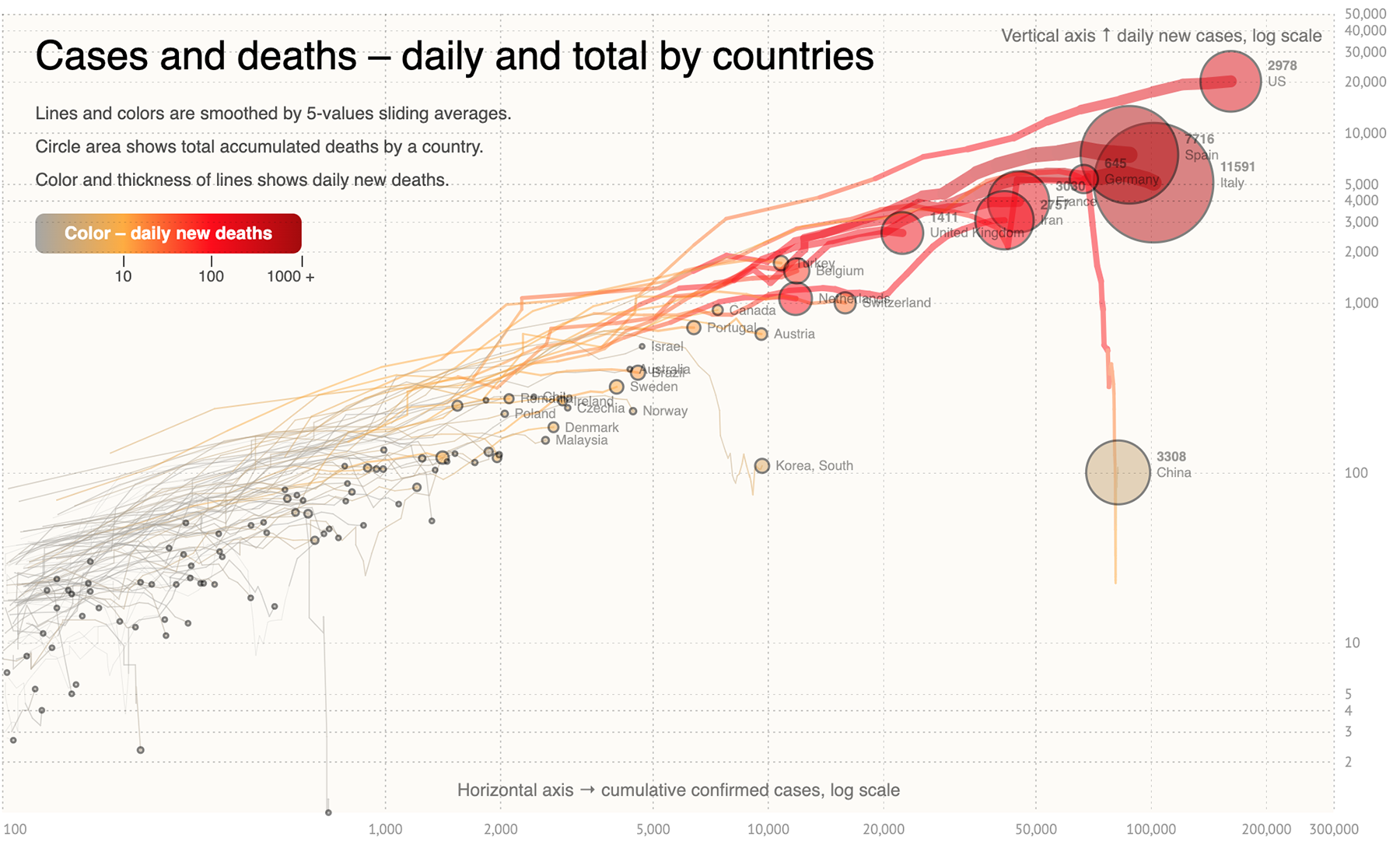
Следующий по популярности формат — график роста заболевших/умерших по странам на таймлайне, который показывает изменение ситуации с течением времени. Например, вот такой, созданный командой «Our world in data» (интерактивная версия ↓):
На горизонтальной оси время, но не календарные даты, а дни, начиная с пятой смерти в стране. На вертикальной — логарифмическая шкала смертей. Это редкий случай, когда логарифмическая шкала по-настоящему уместна. Рост заражений и смертей идёт по экспоненте, и числа разных порядков оказываются близкими друг к другу: где вчера было 10 случаев, там через неделю (или раньше) их уже 100. Обратите внимание на пунктирную разметку, которая показывает на графике зоны разных темпов роста (число удваивается каждый день, раз в два дня, раз в три дня и т. д.) Смертельные случаи отражают ситуацию намного точнее, чем количество заболевших.
На этом графике видны страны с самыми высокими темпами роста:
И страны, которые взяли эпидемию под контроль:
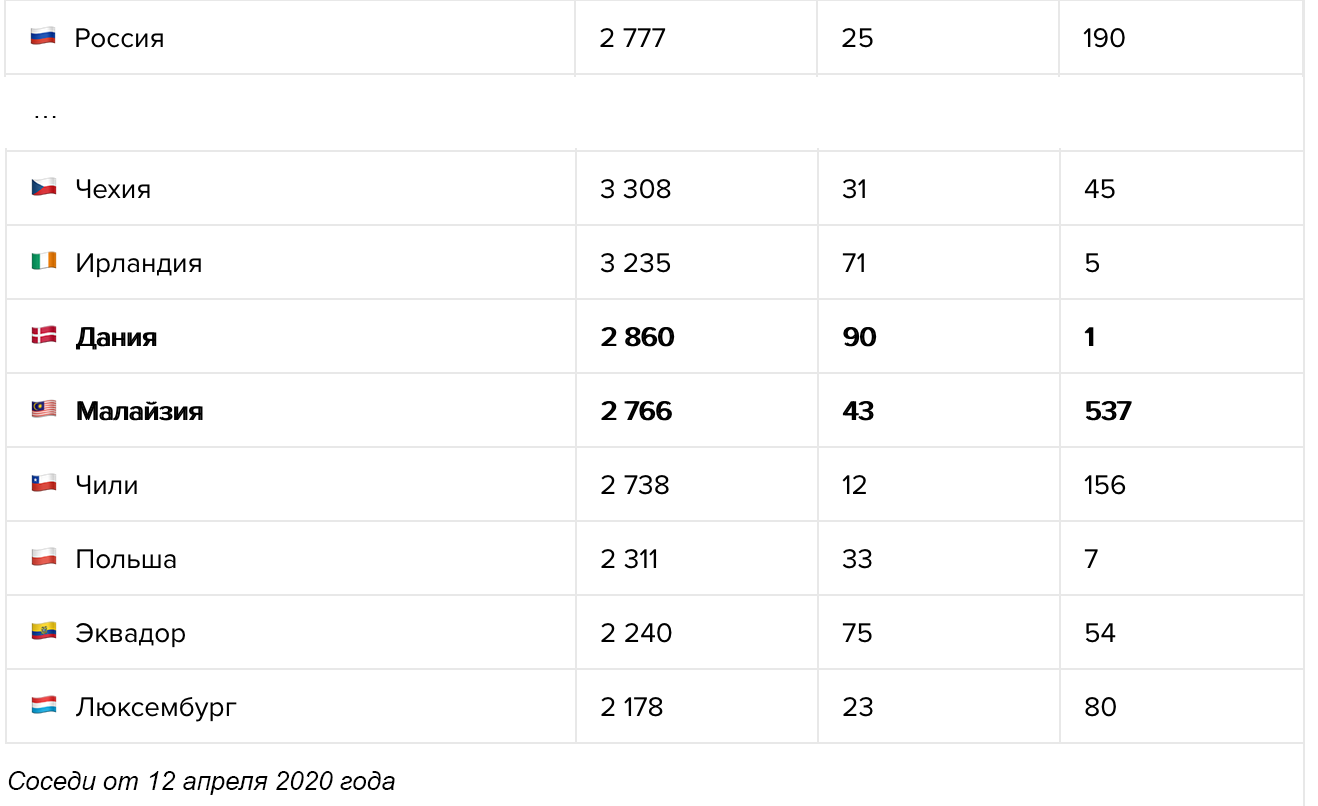
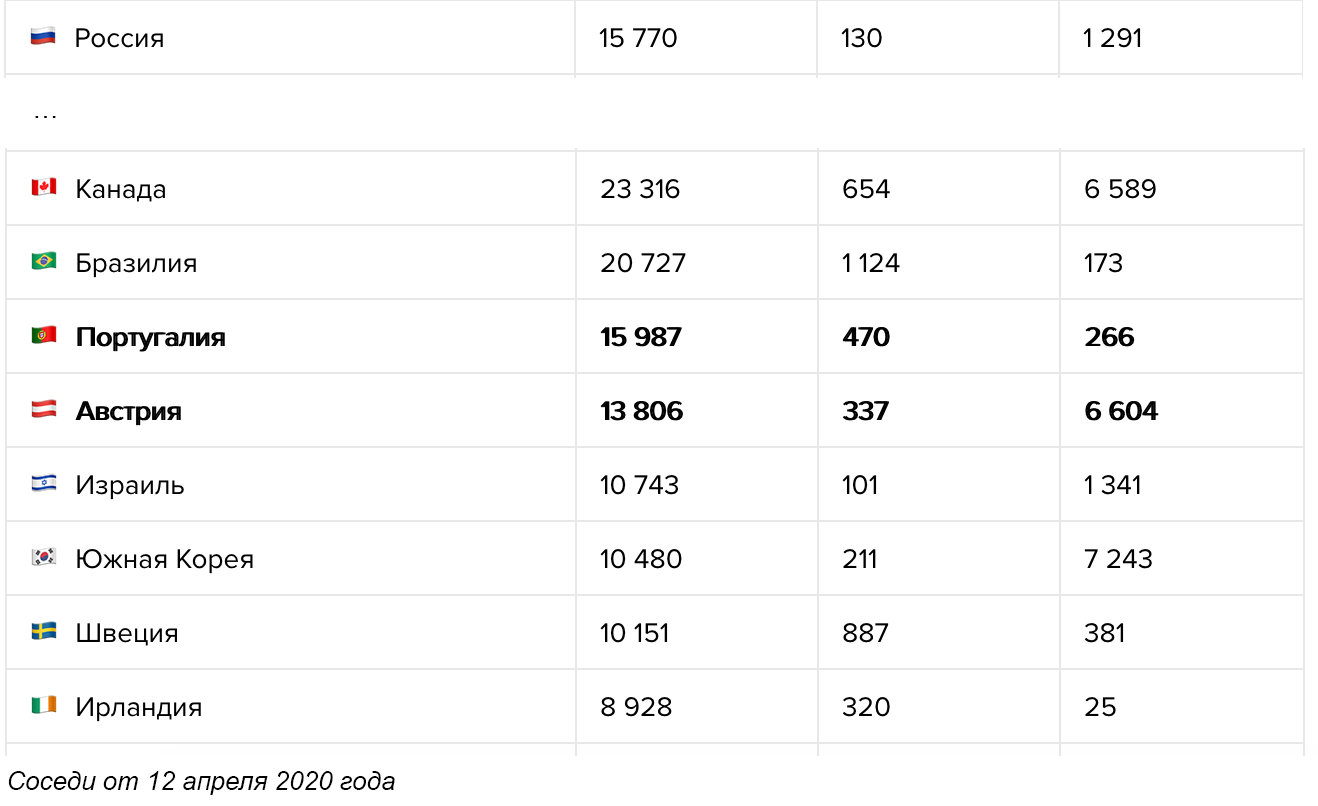
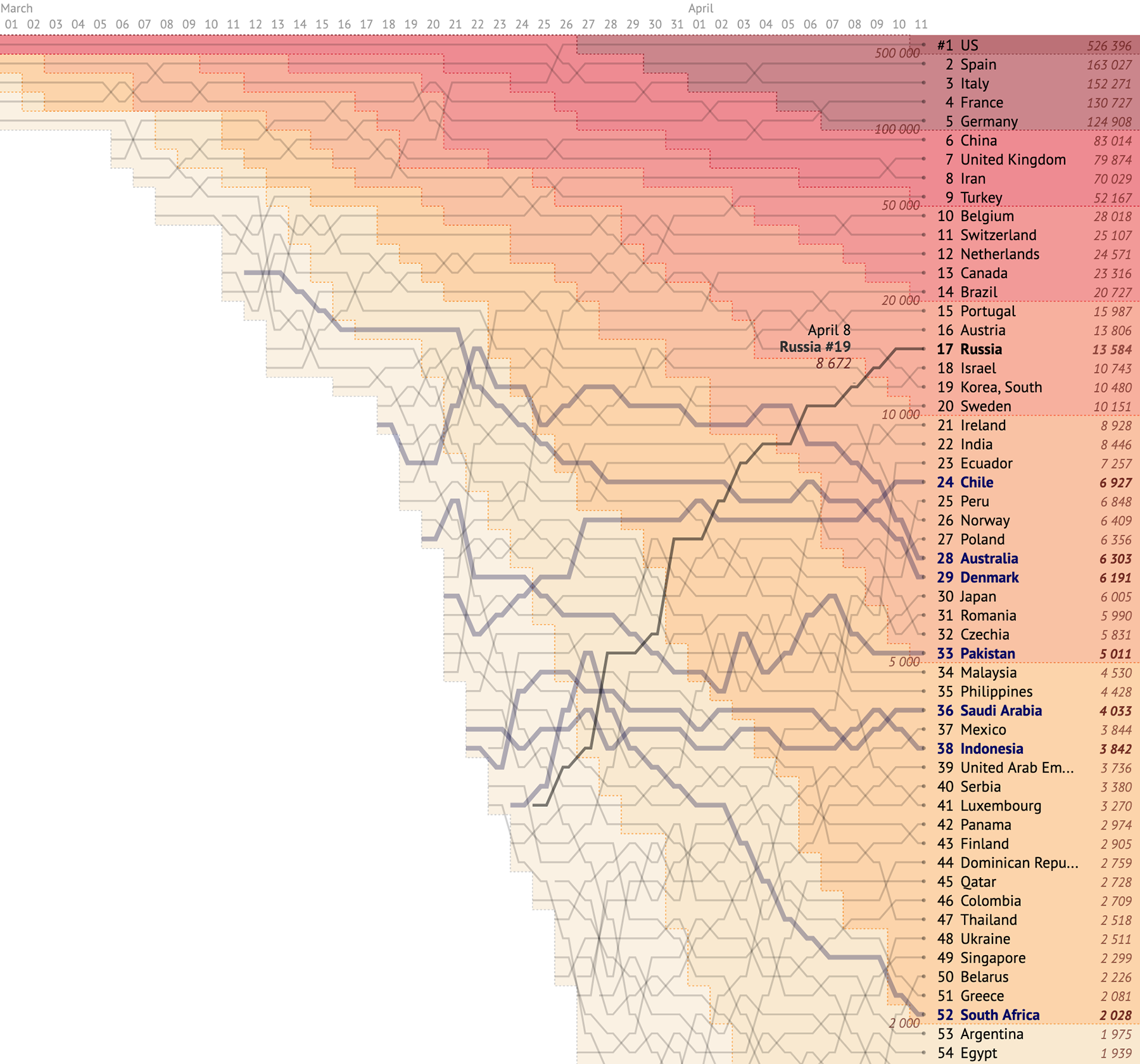
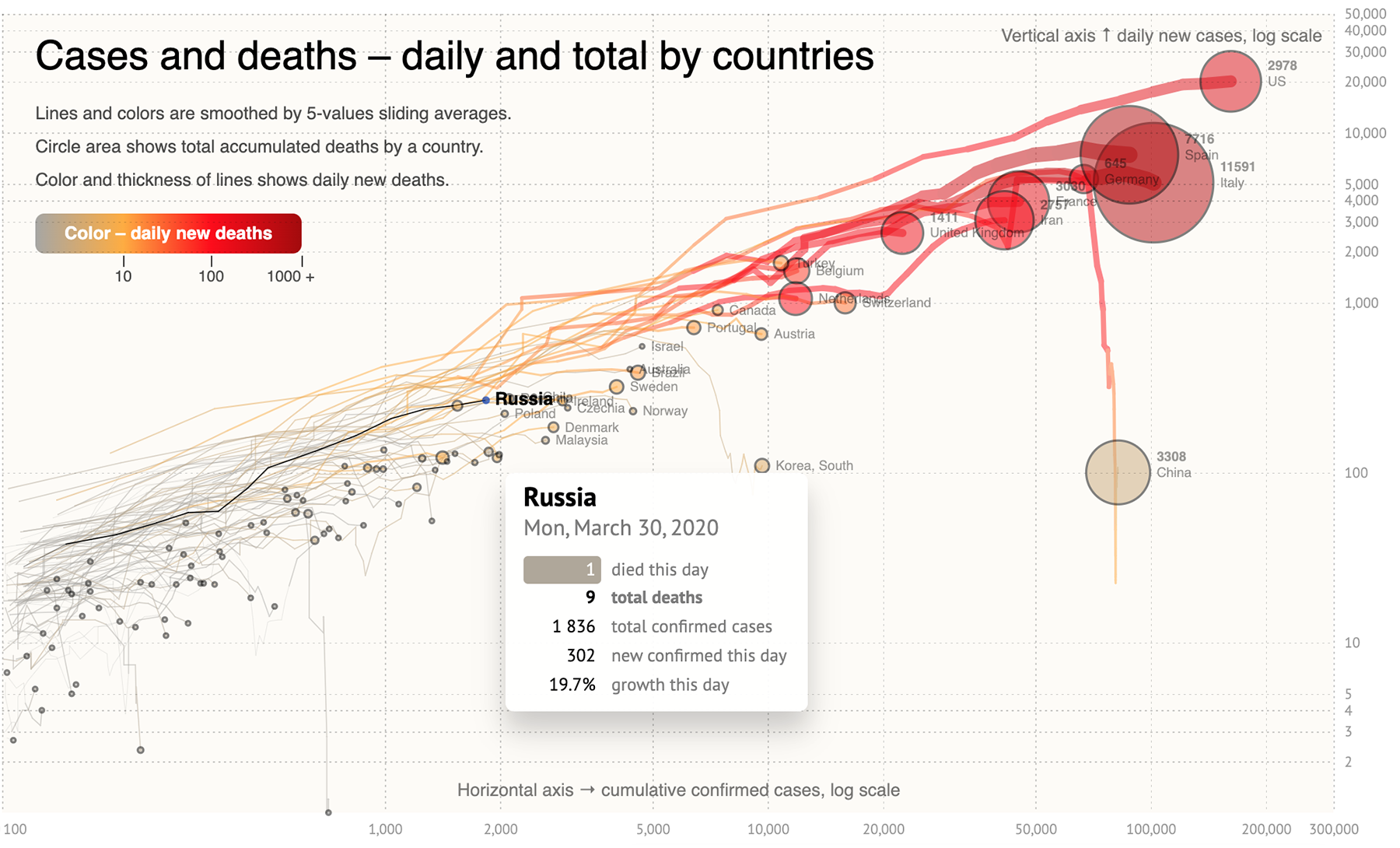
Но как насчёт стран, оказавшихся где-то между? Есть ещё один формат, который отлично проявляет текущую ситуацию, а именно, продолжается ли экспоненциальный рост заболевших в стране или эпидемия замедляется. Это график дневного прироста заболевших против суммарного их количества. Больше всего мне нравится реализация, опубликованная на днях Сергеем Кашиным:
На графике можно отследить момент, когда кривая начинает отклоняться от основного направления вниз — это и есть замедление экспоненциального роста. Не всем странам удаётся удержать это движение (см. Иран, который было нырнул вниз, но снова подтянулся к диагонали), но для большинства стран их прогресс из этого графика становится понятен. Большой плюс этого графика в том, что мы смотрим на зависимость величин, которые измерены одинаковым образом, на их соотношение. И это отчасти нивелирует неточность, заложенную в параметре «количество заболевших», о которой я писала выше. Благодаря этому можно делать выводы о странах, в которых количество смертей ещё недостаточно велико, но количество подтверждённых случаев растёт достаточно быстро:
Помимо суммарного количества заболевших и ежедневного прироста, на графике показаны также суммарное количество смертей (размер кружка) и ежедневный прирост смертей (толщина и цвет линии). Визуализация также снабжена временным слайдером, который можно запустить или подвигать вручную. Итого — пять измерений данных на одном графике. Сергей, снимаю шляпу :-)
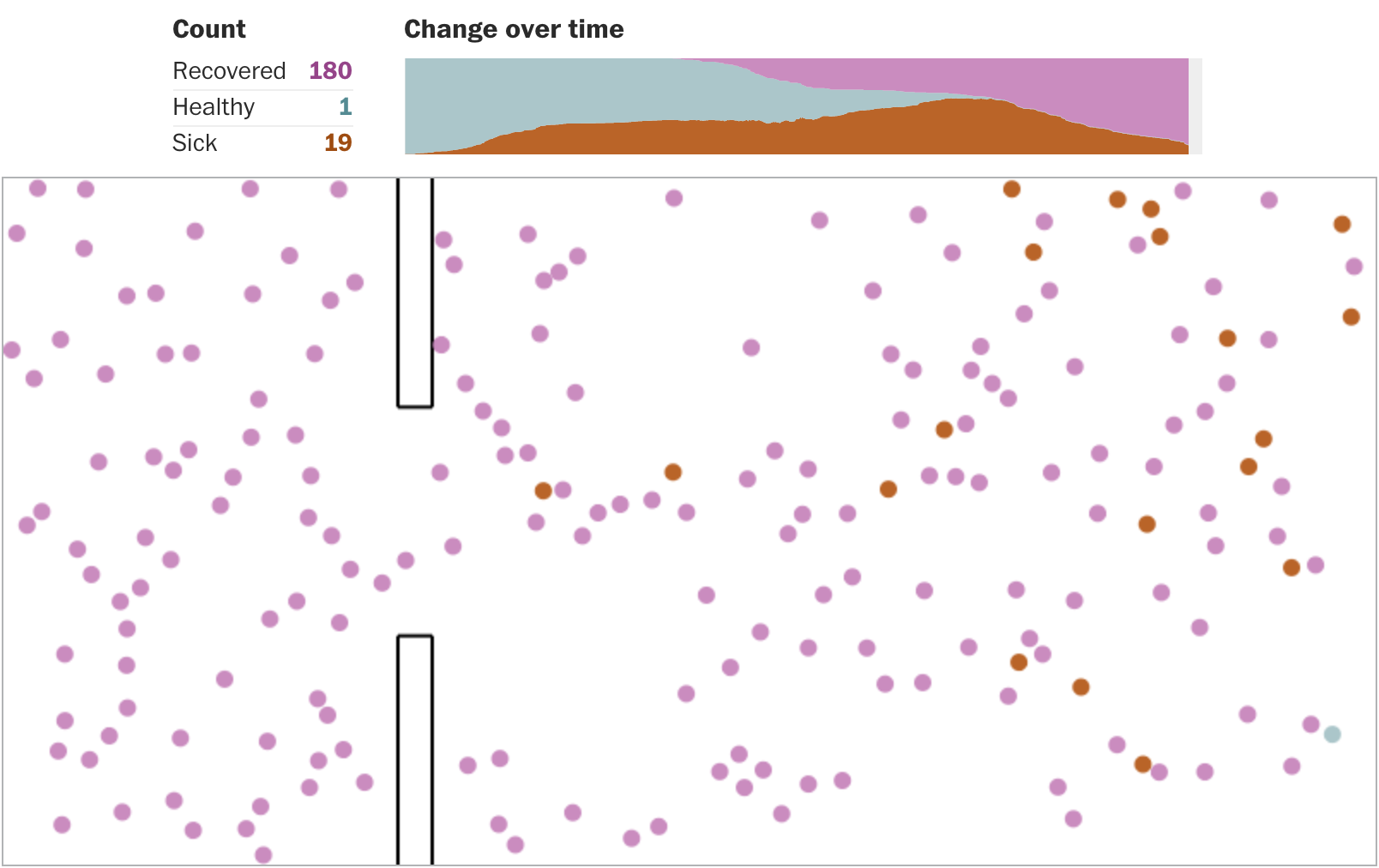
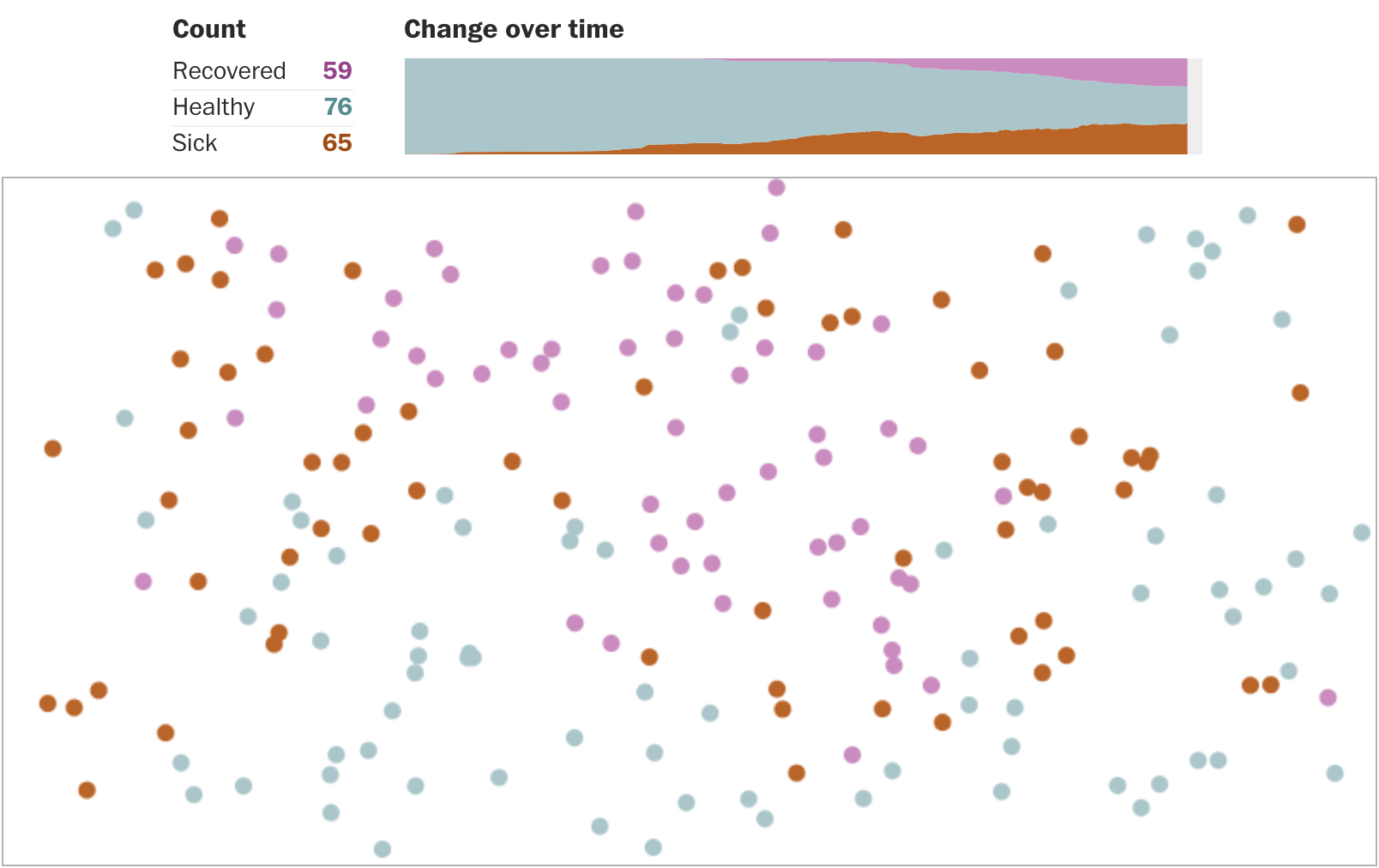
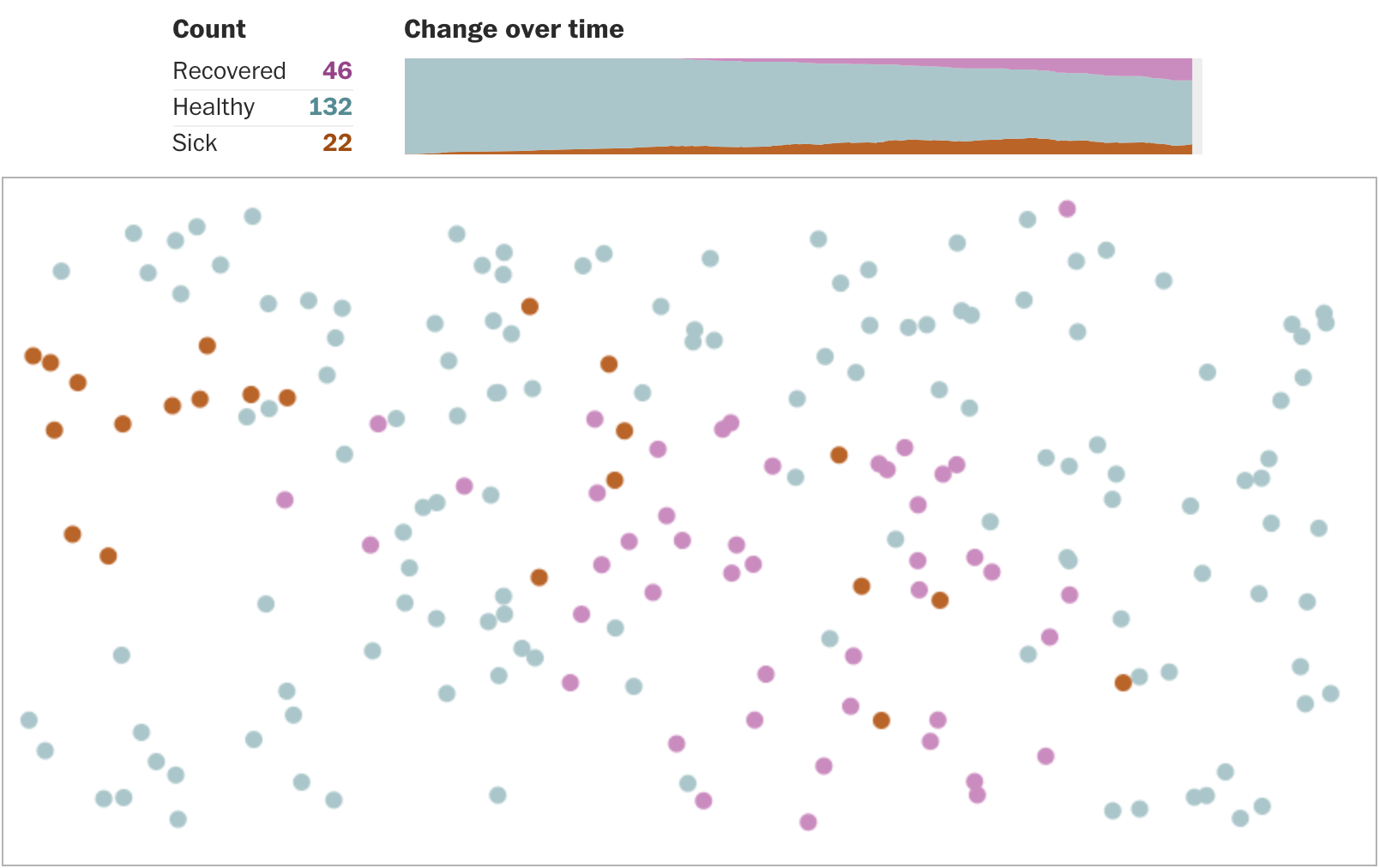
Ещё один жанр, который не могу обойти вниманием, — интерактивные модели. Вашингтон-пост приводит сильно упрощённую демонстрацию влияния мер разной степени жёсткости на темпы распространения инфекции:
В конце статьи можно сравнить между собой графики всех четырёх процессов:
Модель примитивная, и к ней есть вопросы. Но я лично знаю людей, для которых она оказалась достаточным аргументом, чтобы пересмотреть привычки и взгляд на социальное дистанцирование.
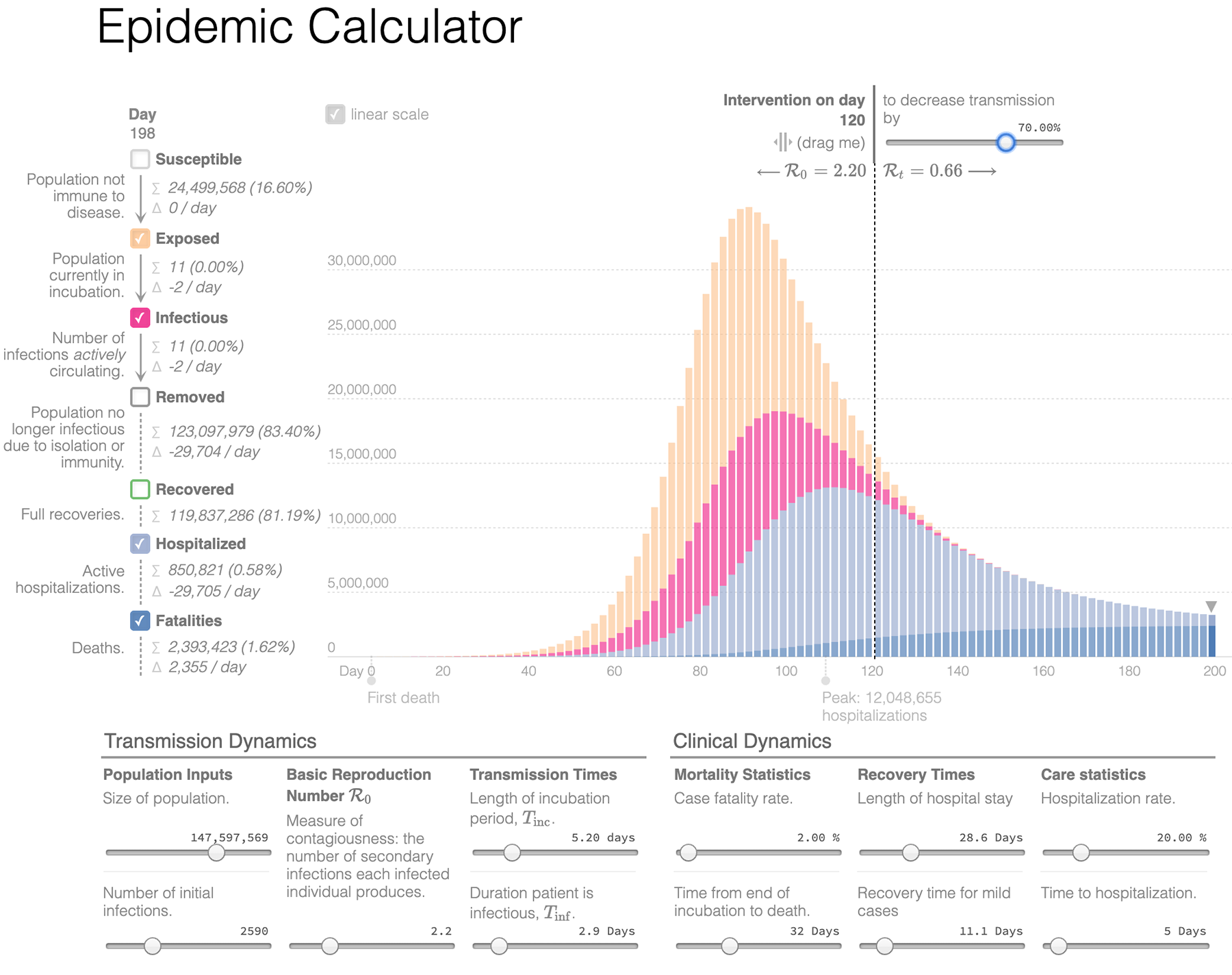
А вот потрясающий калькулятор эпидемии:
Наглядный, быстрый, с большим количеством настроек — настоящий инструмент исследователя. В статье Томаса Пуйо «Молот и танец» показано, как приближая момент и увеличивая степень вмешательства в естественный ход распространения вируса, можно снизить нагрузку на систему здравоохранения с десятков миллионов до десятков тысяч обращений. И как это позволит выиграть время, чтобы встретить врага (коронавирус) во всеоружии.
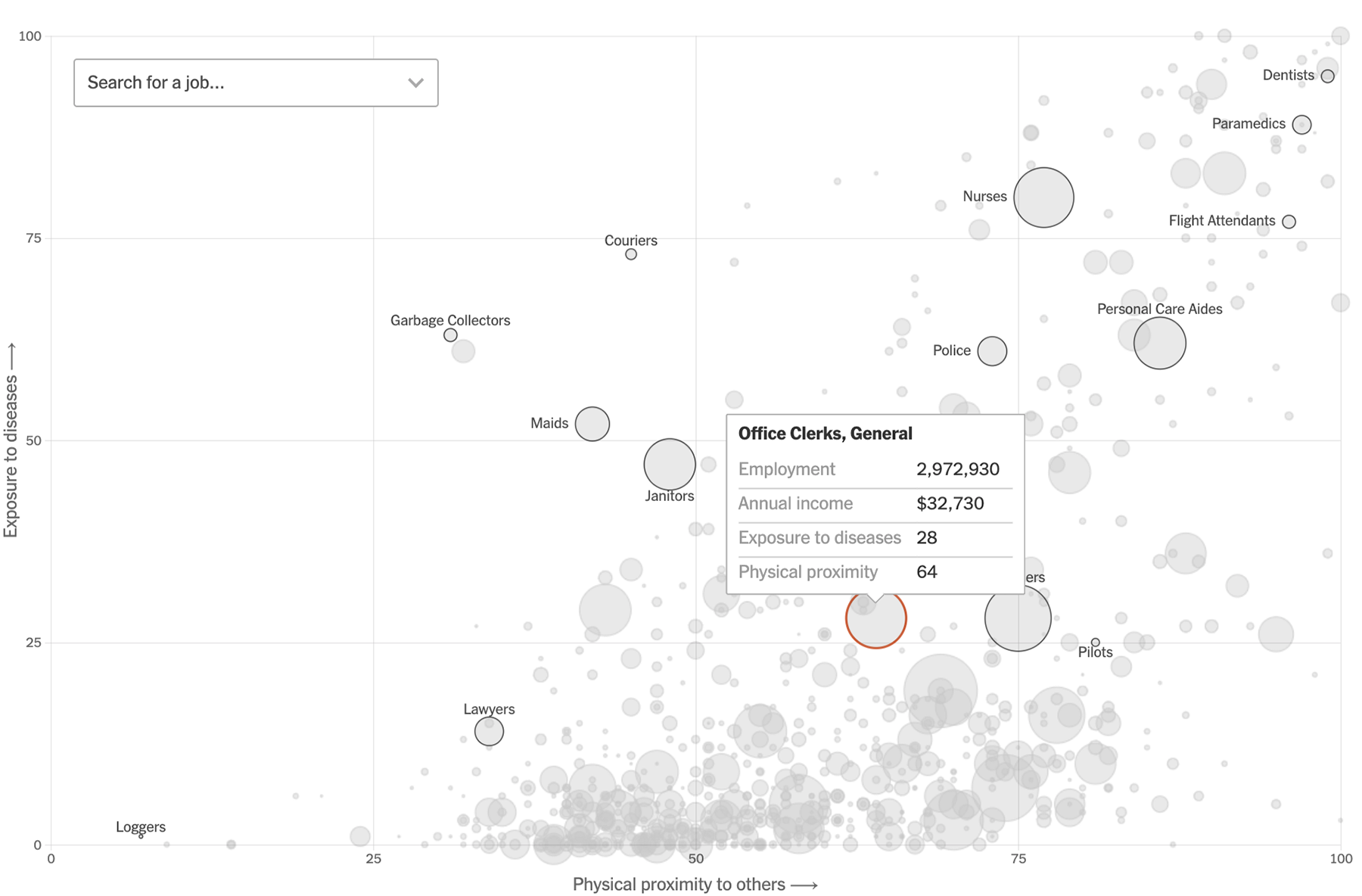
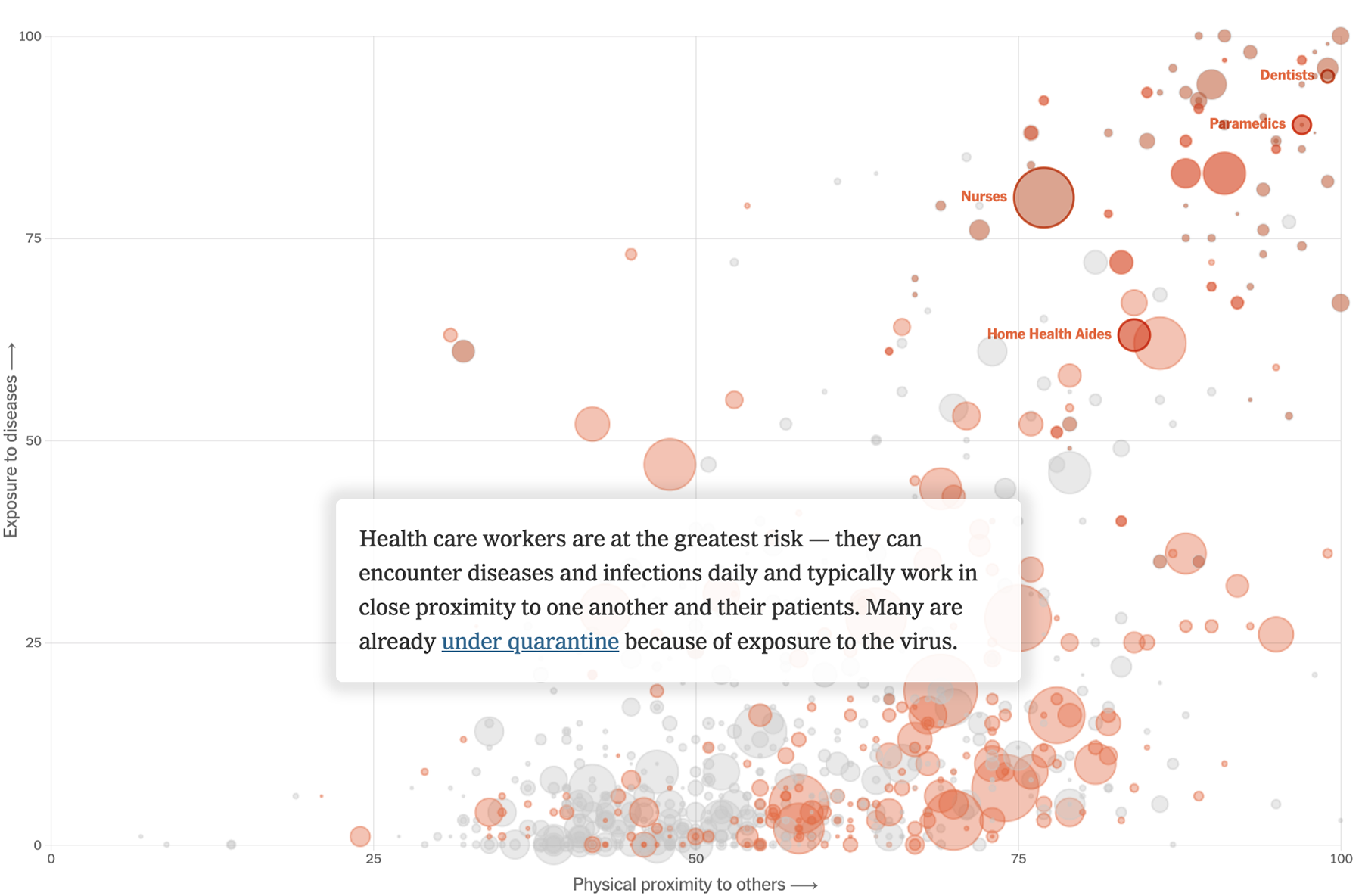
Кстати, о нагрузке на больницы и медперсонал. На визуализации Нью-йорк-таймс показан риск заражения вирусом для разных профессий:
Неудивительно, что доктора (особенно, дантисты и пульмонологи), медсёстры и врачи скорой помощи оказались в самом рисковом, правом верхнем углу графика:
Кстати, это один из немногих графиков, который соотносит события глобального масштаба и личные тревоги: можно вбить в поиск свою профессию и увидеть свои риски на общем фоне. Мне не хватает визуализаций с таким подходом, не хватает возможности оценить риск для себя и близких с учётом географии, пола, возраста, профессии и других нюансов.
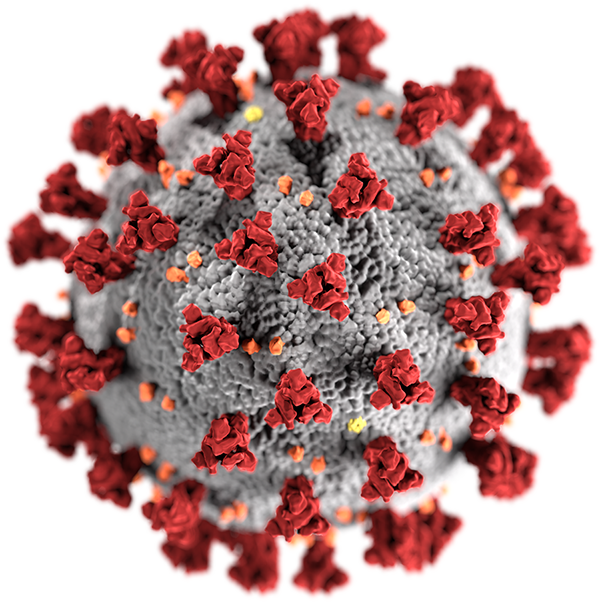
Ну и напоследок, давайте посмотрим врагу в лицо:
Эта иллюстрация вириона SARS-CoV-2 — самое распространённое в сети изображение частицы вируса, который вызывает COVID-19, — создана учёными Центра по контролю и профилактике заболеваний США (CDC).
А вот вирионы снятые через электронный микроскоп. На поверхности частиц видные выступы гликопротеинов, которые напоминают зубцы короны. Отсюда и название всей группы — «коронавирусы»:
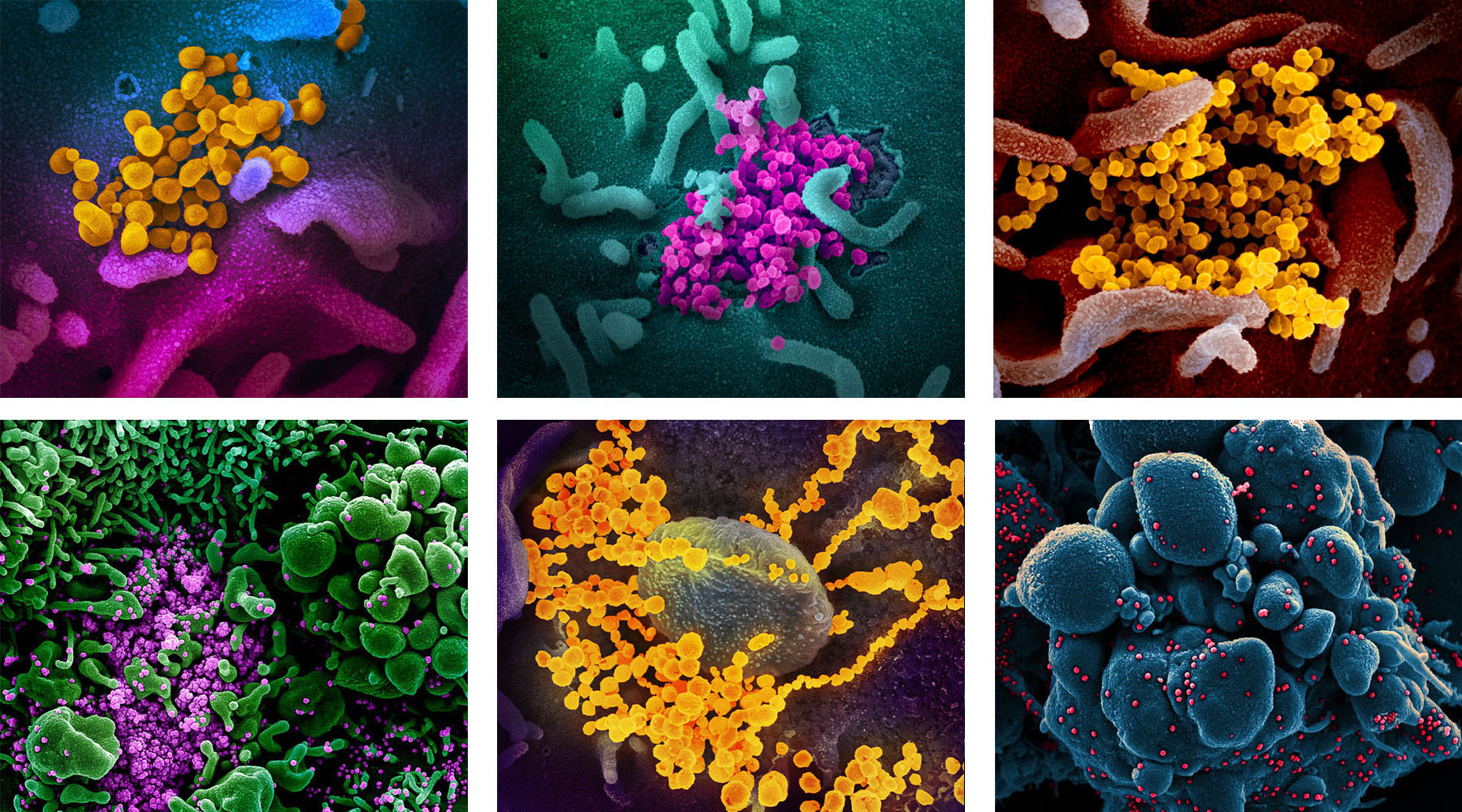
На фликре NIAID целый альбом с красочными микрофотографиями вируса на поражённых клетках:
Если не можете устоять перед потоками информации (как я), лучше потратьте время на внимательное изучение всей этой красоты, чем на очередную горячую новость :-)
Оставайтесь дома. Сохраняйте спокойствие. Будьте здоровы.